Электроника:Переменный ток/Комплексные числа/Арифметика комплексных чисел: различия между версиями
Myagkij (обсуждение | вклад) Нет описания правки |
Нет описания правки |
||
| (не показаны 4 промежуточные версии 1 участника) | |||
| Строка 5: | Строка 5: | ||
=Арифметика комплексных чисел<ref>[https://www.allaboutcircuits.com/textbook/alternating-current/chpt-2/complex-number-arithmetic/ www.allaboutcircuits.com - Complex Number Arithmetic]</ref>= | =Арифметика комплексных чисел<ref>[https://www.allaboutcircuits.com/textbook/alternating-current/chpt-2/complex-number-arithmetic/ www.allaboutcircuits.com - Complex Number Arithmetic]</ref>= | ||
Поскольку комплексные числа, как и | Поскольку [[комплексные числа]], как и [[скаляр]]ные, – полноценные математические объекты, то их можно складывать, вычитать, умножать, делить, возводить в квадрат, инвертировать и т.д., как и любые другие числа. | ||
Хотя нужно уметь работать с комплексными числами и без клавиатурных помощников, настоятельно советую обзавестись инженерным калькулятором, способным выполнять арифметические операции с комплексными числами. Тогда ваше изучение цепей переменного тока будет ещё более приятным, так как ручные расчёты проделываются всё-таки несколько дольше. | Некоторые [[инженерные калькуляторы]] умеют выполнять подобные операции непосредственно с двумя или более [[комплексными числами]]. Но также не помешает знать, как это можно делать и «на бумаге». В этом разделе разберём, как вручную выполняются основные операции. | ||
Хотя нужно уметь работать с [[комплексными числами]] и без клавиатурных помощников, настоятельно советую обзавестись [[инженерным калькулятором]], способным выполнять арифметические операции с [[комплексными числами]]. Тогда ваше изучение цепей [[переменного тока]] будет ещё более приятным, так как ручные расчёты проделываются всё-таки несколько дольше. | |||
== Сложение и вычитание комплексных чисел в алгебраической форме записи == | == Сложение и вычитание комплексных чисел в алгебраической форме записи == | ||
Складывать/вычитать комплексные числа в алгебраической форме записи до безобразия просто. При сложении сначала сложите действительные составляющие комплексных чисел – так определится действительная составляющую суммы. Ну и затем сложите мнимые составляющие комплексных чисел, чтобы определить мнимую составляющую суммы: | Складывать/вычитать [[комплексные числа]] в [[алгебраической форме]] записи до безобразия просто. При сложении сначала сложите действительные составляющие [[комплексных чисел]] – так определится действительная составляющую суммы. Ну и затем сложите [[мнимые составляющие]] [[комплексных чисел]], чтобы определить [[мнимую составляющую]] суммы: | ||
[[File:Складывание комплексных чисел в алгебраической форме записи_1_08062021_1500.png|frame|center|Рис. 1. Складывание комплексных чисел в алгебраической форме записи.]] | [[File:Складывание комплексных чисел в алгебраической форме записи_1_08062021_1500.png|frame|center|'''Рис. 1.''' Складывание комплексных чисел в алгебраической форме записи.|alt=Рис. 1. Складывание комплексных чисел в алгебраической форме записи.]] | ||
При вычитании комплексных чисел в алгебраической форме просто сначала вычтите вещественную составляющую второго комплексного числа из вещественной составляющей первого, чтобы получить вещественную составляющую разности. И затем вычтите мнимую составляющую второго комплексного числа из мнимой составляющей первого, чтобы получить мнимую составляющую разности: | При вычитании [[комплексных чисел]] в [[алгебраической форме]] просто сначала вычтите вещественную составляющую второго [[комплексного числа]] из вещественной составляющей первого, чтобы получить вещественную составляющую разности. И затем вычтите [[мнимую составляющую]] второго [[комплексного числа]] из мнимой составляющей первого, чтобы получить [[мнимую составляющую]] разности: | ||
[[File:Вычитание комплексных чисел в алгебраической форме записи_2_08062021_1500.png|frame|center|Рис. 2. Вычитание комплексных чисел в алгебраической форме записи.]] | [[File:Вычитание комплексных чисел в алгебраической форме записи_2_08062021_1500.png|frame|center|'''Рис. 2.''' Вычитание комплексных чисел в алгебраической форме записи.|alt=Рис. 2. Вычитание комплексных чисел в алгебраической форме записи.]] | ||
== Умножение и деление комплексных чисел в полярной форме записи == | == Умножение и деление комплексных чисел в полярной форме записи == | ||
Для обычного умножения и деления предпочтительнее использовать полярную нотацию. При умножении комплексных чисел в полярной форме просто перемножьте полярные величины комплексных чисел, чтобы определить полярную величину произведения, и затем сложите углы комплексных чисел, чтобы определить угол произведения: | Для обычного умножения и деления предпочтительнее использовать полярную нотацию. При умножении [[комплексных чисел]] в [[полярной форме]] просто перемножьте полярные величины [[комплексных чисел]], чтобы определить полярную величину произведения, и затем сложите углы [[комплексных чисел]], чтобы определить угол произведения: | ||
[[File:Умножение комплексных чисел в полярной форме записи_3_08062021_1503.png|frame|center|Рис. 3. Умножение комплексных чисел в полярной форме записи.]] | [[File:Умножение комплексных чисел в полярной форме записи_3_08062021_1503.png|frame|center|'''Рис. 3.''' Умножение комплексных чисел в полярной форме записи.|alt=Рис. 3. Умножение комплексных чисел в полярной форме записи.]] | ||
{{ads2}} | {{ads2}} | ||
Делить комплексные числа в полярной форме легко и просто: просто разделите полярную величину первого комплексного числа на полярную величину второго комплексного числа, чтобы получить полярную величину частного. Потом вычтите угол второго комплексного числа из угла первого комплексного числа, чтобы получить угол частного: | Делить [[комплексные числа]] в [[полярной форме]] легко и просто: просто разделите полярную величину первого [[комплексного числа]] на полярную величину второго [[комплексного числа]], чтобы получить полярную величину частного. Потом вычтите угол второго [[комплексного числа]] из угла первого [[комплексного числа]], чтобы получить угол частного: | ||
[[File:Деление комплексных чисел в полярной форме записи_4_08062021_1501.png|frame|center|Рис. 4. Деление комплексных чисел в полярной форме записи.]] | [[File:Деление комплексных чисел в полярной форме записи_4_08062021_1501.png|frame|center|'''Рис. 4.''' Деление комплексных чисел в полярной форме записи.|alt=Рис. 4. Деление комплексных чисел в полярной форме записи.]] | ||
Чтобы получить обратное или «инвертированное» (1/x) комплексное число, просто представьте скалярную единицу в полярной форме записи (это будет не что иное, как комплексное число, у которого вещественная составляющая равна 1, а мнимая | Чтобы получить обратное или «инвертированное» (1/x) [[комплексное число]], просто представьте скалярную единицу в полярной форме записи (это будет не что иное, как [[комплексное число]], у которого [[вещественная составляющая]] равна 1, а мнимая составляющая ∠0°) и затем разделите на [[комплексное число]] x: | ||
[[File:Инвертирование комплексных чисел в полярной форме записи_5_08062021_1501.png|frame|center|Рис. 5. Инвертирование комплексных чисел в полярной форме записи.]] | [[File:Инвертирование комплексных чисел в полярной форме записи_5_08062021_1501.png|frame|center|'''Рис. 5.''' Инвертирование комплексных чисел в полярной форме записи.|alt=Рис. 5. Инвертирование комплексных чисел в полярной форме записи.]] | ||
Это основные операции, которые вам понадобятся, чтобы управлять комплексными числами при анализе цепей переменного тока. Понятное дело, что операции с комплексными числами никоим образом не ограничиваются только сложением, вычитанием, умножением, делением и инверсией. | Это основные операции, которые вам понадобятся, чтобы управлять [[комплексными числами]] при анализе цепей [[переменного тока]]. Понятное дело, что операции с [[комплексными числами]] никоим образом не ограничиваются только сложением, вычитанием, умножением, делением и инверсией. | ||
Практически любая арифметическая операция, которая может быть выполнена со скалярными числами, может выполняться и с комплексными числами, как-то: возведение в степень, извлечение корня, решение систем уравнений с комплексными коэффициентами и даже тригонометрические функции (хотя, что касается комплексной тригонометрии, то там понадобятся так называемые гиперболические функции, но, пожалуй, не будем сейчас вдаваться в такие дебри, это явно выходит за рамки нашего курса). | Практически любая арифметическая операция, которая может быть выполнена со [[скалярными числами]], может выполняться и с [[комплексными числами]], как-то: возведение в степень, извлечение корня, решение систем уравнений с комплексными коэффициентами и даже [[тригонометрические функции]] (хотя, что касается комплексной тригонометрии, то там понадобятся так называемые [[гиперболические функции]], но, пожалуй, не будем сейчас вдаваться в такие дебри, это явно выходит за рамки нашего курса). | ||
В общем, освойте для комплексных чисел это основные (и несложные) арифметические операции сложения, вычитания, умножения, деления и инверсии, и у вас не будет проблем с анализом цепей переменного тока, даже если под рукой не окажется продвинутого калькулятора. | В общем, освойте для [[комплексных чисел]] это основные (и несложные) арифметические операции сложения, вычитания, умножения, деления и инверсии, и у вас не будет проблем с анализом цепей [[переменного тока]], даже если под рукой не окажется [[продвинутого калькулятора]]. | ||
== Итог == | == Итог == | ||
* Чтобы сложить комплексные числа в алгебраической форме, отдельно сложите действительные составляющие и отдельно сложите мнимые составляющие. Вычитание производится аналогично. | * Чтобы сложить [[комплексные числа]] в [[алгебраической форме]], отдельно сложите действительные составляющие и отдельно сложите [[мнимые составляющие]]. Вычитание производится аналогично. | ||
* Чтобы перемножить комплексные числа в полярной форме, перемножьте величины и сложите углы. Чтобы разделить, разделите величины и вычтите один угол из другого. | * Чтобы перемножить [[комплексные числа]] в полярной форме, перемножьте величины и сложите углы. Чтобы разделить, разделите величины и вычтите один угол из другого. | ||
=См.также= | =См.также= | ||
=Внешние ссылки= | =Внешние ссылки= | ||
| Строка 55: | Строка 56: | ||
<references /> | <references /> | ||
{{Навигационная таблица/Электроника}} | {{Навигационная таблица/Портал/Электроника}} | ||
[[Категория:Переменный ток]] | |||
[[Категория:Комплексные числа]] | |||
[[Категория:Арифметика комплексных чисел]] | |||
[[Категория:Теория]] | |||
[[Категория:Теория по электронике]] | |||
Текущая версия от 21:40, 22 мая 2023
Арифметика комплексных чисел[1]
Поскольку комплексные числа, как и скалярные, – полноценные математические объекты, то их можно складывать, вычитать, умножать, делить, возводить в квадрат, инвертировать и т.д., как и любые другие числа.
Некоторые инженерные калькуляторы умеют выполнять подобные операции непосредственно с двумя или более комплексными числами. Но также не помешает знать, как это можно делать и «на бумаге». В этом разделе разберём, как вручную выполняются основные операции.
Хотя нужно уметь работать с комплексными числами и без клавиатурных помощников, настоятельно советую обзавестись инженерным калькулятором, способным выполнять арифметические операции с комплексными числами. Тогда ваше изучение цепей переменного тока будет ещё более приятным, так как ручные расчёты проделываются всё-таки несколько дольше.
Сложение и вычитание комплексных чисел в алгебраической форме записи
Складывать/вычитать комплексные числа в алгебраической форме записи до безобразия просто. При сложении сначала сложите действительные составляющие комплексных чисел – так определится действительная составляющую суммы. Ну и затем сложите мнимые составляющие комплексных чисел, чтобы определить мнимую составляющую суммы:
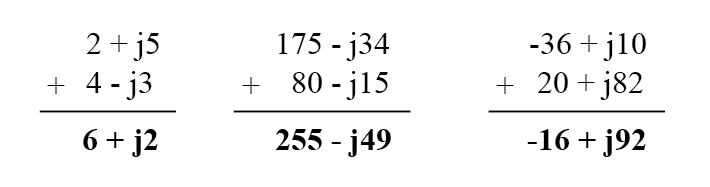
При вычитании комплексных чисел в алгебраической форме просто сначала вычтите вещественную составляющую второго комплексного числа из вещественной составляющей первого, чтобы получить вещественную составляющую разности. И затем вычтите мнимую составляющую второго комплексного числа из мнимой составляющей первого, чтобы получить мнимую составляющую разности:
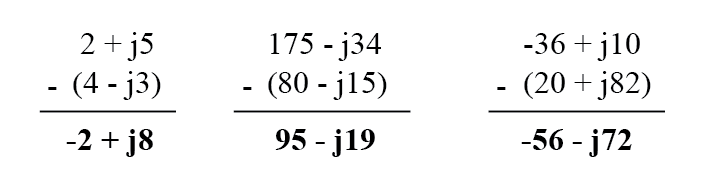
Умножение и деление комплексных чисел в полярной форме записи
Для обычного умножения и деления предпочтительнее использовать полярную нотацию. При умножении комплексных чисел в полярной форме просто перемножьте полярные величины комплексных чисел, чтобы определить полярную величину произведения, и затем сложите углы комплексных чисел, чтобы определить угол произведения:
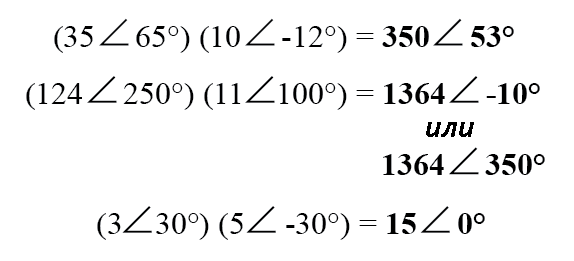
Делить комплексные числа в полярной форме легко и просто: просто разделите полярную величину первого комплексного числа на полярную величину второго комплексного числа, чтобы получить полярную величину частного. Потом вычтите угол второго комплексного числа из угла первого комплексного числа, чтобы получить угол частного:
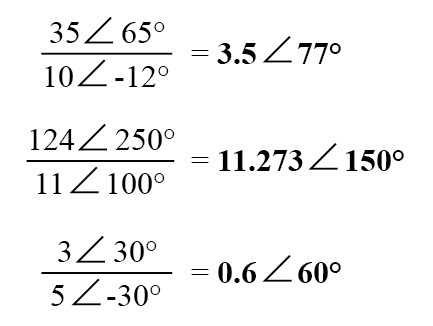
Чтобы получить обратное или «инвертированное» (1/x) комплексное число, просто представьте скалярную единицу в полярной форме записи (это будет не что иное, как комплексное число, у которого вещественная составляющая равна 1, а мнимая составляющая ∠0°) и затем разделите на комплексное число x:
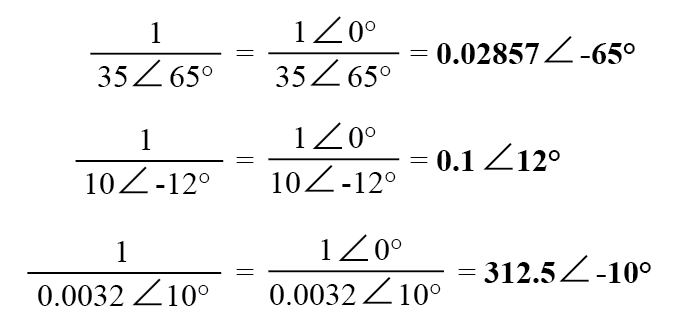
Это основные операции, которые вам понадобятся, чтобы управлять комплексными числами при анализе цепей переменного тока. Понятное дело, что операции с комплексными числами никоим образом не ограничиваются только сложением, вычитанием, умножением, делением и инверсией.
Практически любая арифметическая операция, которая может быть выполнена со скалярными числами, может выполняться и с комплексными числами, как-то: возведение в степень, извлечение корня, решение систем уравнений с комплексными коэффициентами и даже тригонометрические функции (хотя, что касается комплексной тригонометрии, то там понадобятся так называемые гиперболические функции, но, пожалуй, не будем сейчас вдаваться в такие дебри, это явно выходит за рамки нашего курса).
В общем, освойте для комплексных чисел это основные (и несложные) арифметические операции сложения, вычитания, умножения, деления и инверсии, и у вас не будет проблем с анализом цепей переменного тока, даже если под рукой не окажется продвинутого калькулятора.
Итог
- Чтобы сложить комплексные числа в алгебраической форме, отдельно сложите действительные составляющие и отдельно сложите мнимые составляющие. Вычитание производится аналогично.
- Чтобы перемножить комплексные числа в полярной форме, перемножьте величины и сложите углы. Чтобы разделить, разделите величины и вычтите один угол из другого.
См.также
Внешние ссылки