Электроника:Переменный ток/Основы теории переменного тока/Фаза переменного тока: различия между версиями
Myagkij (обсуждение | вклад) (Новая страница: «{{Панель управления/Электроника}} {{Перевод от valemak}} {{Myagkij-редактор}} =<ref>[https://www.allaboutcircuits.com...») |
Нет описания правки |
||
| (не показано 6 промежуточных версий 1 участника) | |||
| Строка 3: | Строка 3: | ||
{{Myagkij-редактор}} | {{Myagkij-редактор}} | ||
=<ref>[https://www.allaboutcircuits.com/textbook/alternating-current/chpt-1/ac-phase/ www.allaboutcircuits.com - AC Phase]</ref>= | =Фаза переменного тока<ref>[https://www.allaboutcircuits.com/textbook/alternating-current/chpt-1/ac-phase/ www.allaboutcircuits.com - AC Phase]</ref>= | ||
Все начинает усложняться, когда необходимо увязать две или более переменных для напряжения или силы тока, которые не согласованы друг с другом. Под «несогласованностью» подразумевается, что две формы сигнала не синхронизированы: их пики и нулевые точки не совпадают в одни и те же моменты времени. Если эту ситуацию отобразить в виде графика, то выглядеть это будет как-то вот так: | |||
[[File:Фазы двух волн не совпадают_1_08062021_1349.png|frame|center|'''Рис. 1.''' Фазы двух волн не совпадают.|alt=Рис. 1. Фазы двух волн не совпадают.]] | |||
Две волны, показанные выше (A и B), имеют одинаковую амплитуду и частоту, но они не совпадают друг с другом. Технически это называется фазовым сдвигом. Ранее мы видели, как можно построить «[[синусоидальную волну]]», вычислив [[тригонометрическую функцию]] [[синус]]а для углов от 0° до 360°, то есть полного круга. | |||
Начальной точкой синусоидальной волны была нулевая амплитуда при 0°, прогрессирующая до полной положительной амплитуды при 90°, затем снова достигался ноль при 180°, потом полная отрицательная амплитуда при 270° и возвращение к начальной нулевой точке при 360°. | |||
Мы можем использовать эту угловую шкалу вдоль горизонтальной оси нашего графика, чтобы показать, насколько первая волна не совпадает со второй: | |||
[[File:Волна A опережает волну B на 45_2_08062021_1349.png|frame|center|'''Рис. 2.''' Волна A опережает волну B на 45°.|alt=Рис. 2. Волна A опережает волну B на 45°.]] | |||
Сдвиг между этими двумя волнами составляет около 45°, волна «A» опережает волну «B». Выборка различных вариантов фазовых сдвигов представлена на следующих графиках, чтобы лучше проиллюстрировать эту концепцию: | |||
[[File:Примеры фазовых сдвигов_3_08062021_1349.jpg|frame|center|'''Рис. 3.''' Примеры фазовых сдвигов.|alt=Рис. 3. Примеры фазовых сдвигов.]] | |||
Поскольку формы сигналов в приведённых выше примерах имеют одинаковую частоту, они будут отличаться в каждом шаге на одинаковую угловую величину в каждый момент времени. По этой причине можно выразить фазовый сдвиг для двух или более сигналов одной и той же частоты как постоянную величину для всей волны, а не заново каждый раз вычислять сдвиг между любыми двумя точками вдоль волн. | |||
{{ads2}} | |||
То есть можно уверенно сказать что-то вроде такого: «Напряжение A сдвинуто по фазе на 45° по сравнению с напряжением В». Тот сигнал, что на графике впереди, называется опережающим, а тот, что позади – отстающим. | |||
Фазовый сдвиг, как и напряжение, всегда является измерением чего-либо в количестве двух (или более чем двух). Т.е., чтобы говорить о фазовом сдвиге, нужно как минимум две волны. На самом деле не существует такой вещи, как форма волны с абсолютной фазой, потому что для фазы нет универсального эталона. | |||
Обычно при анализе цепей переменного тока форма волны для напряжения [[источника питания]] используется в качестве эталона для фазы, это напряжение указано как «*** вольт при 0°». Любое другое переменное напряжение или ток в этой цепи будет иметь фазовый сдвиг, выраженный относительно указанного напряжения источника. | |||
Это как раз то, из-за чего расчёты цепей переменного тока более сложны, чем для постоянного тока. При применении [[закона Ома]] и [[правил Кирхгофа]] величины переменного напряжения и тока должны отражать как фазовый сдвиг, так и амплитуду. Математические операции сложения, вычитания, умножения и деления должны оперировать этими величинами фазового сдвига (и амплитуды). | |||
К счастью, в математике есть [[комплексные числа]], идеально подходящие для задачи одновременного представления в одной переменной и амплитуды и фазы. | |||
Поскольку для понимания цепей [[переменного тока]] так важны [[комплексные числа]], в следующей главе мы их рассмотрим подробнее. | |||
==Итог== | |||
* [[Фазовый сдвиг]] – это когда две (или более) формы сигналов (волн) не совпадают друг с другом. | |||
* Величина [[фазового сдвига]] между двумя волнами может быть выражена в градусах, если разметить в градусах горизонтальную ось графика формы волны, используемую при построении тригонометрической синусоидальной функции. | |||
* Опережающая волна – это та, которая находится по времени впереди в своей эволюции относительно другой волны. Отстающий сигнал – тот, что идёт позади опережающего. Пример: | |||
[[File:Опережающая и отстающая волны_4_08062021_1350.png|frame|center|'''Рис. 4.''' Опережающая и отстающая волны (сигналы).|alt=Рис. 4. Опережающая и отстающая волны (сигналы).]] | |||
* Точные расчёты для анализа цепей переменного тока предполагают учёт как амплитуды, так и фазового сдвига формы волны для напряжения и тока. Это требует использования специального математического аппарата, известного как [[комплексные числа]]. | |||
=См.также= | =См.также= | ||
=Внешние ссылки= | =Внешние ссылки= | ||
| Строка 15: | Строка 55: | ||
<references /> | <references /> | ||
{{Навигационная таблица/Электроника}} | {{Навигационная таблица/Портал/Электроника}} | ||
[[Категория:Переменный ток]] | |||
[[Категория:Основы теории переменного тока]] | |||
[[Категория:Фаза переменного тока]] | |||
[[Категория:Теория]] | |||
[[Категория:Теория по электронике]] | |||
Текущая версия от 21:41, 22 мая 2023
Фаза переменного тока[1]
Все начинает усложняться, когда необходимо увязать две или более переменных для напряжения или силы тока, которые не согласованы друг с другом. Под «несогласованностью» подразумевается, что две формы сигнала не синхронизированы: их пики и нулевые точки не совпадают в одни и те же моменты времени. Если эту ситуацию отобразить в виде графика, то выглядеть это будет как-то вот так:
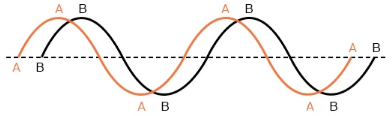
Две волны, показанные выше (A и B), имеют одинаковую амплитуду и частоту, но они не совпадают друг с другом. Технически это называется фазовым сдвигом. Ранее мы видели, как можно построить «синусоидальную волну», вычислив тригонометрическую функцию синуса для углов от 0° до 360°, то есть полного круга.
Начальной точкой синусоидальной волны была нулевая амплитуда при 0°, прогрессирующая до полной положительной амплитуды при 90°, затем снова достигался ноль при 180°, потом полная отрицательная амплитуда при 270° и возвращение к начальной нулевой точке при 360°.
Мы можем использовать эту угловую шкалу вдоль горизонтальной оси нашего графика, чтобы показать, насколько первая волна не совпадает со второй:
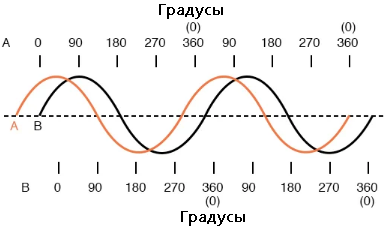
Сдвиг между этими двумя волнами составляет около 45°, волна «A» опережает волну «B». Выборка различных вариантов фазовых сдвигов представлена на следующих графиках, чтобы лучше проиллюстрировать эту концепцию:
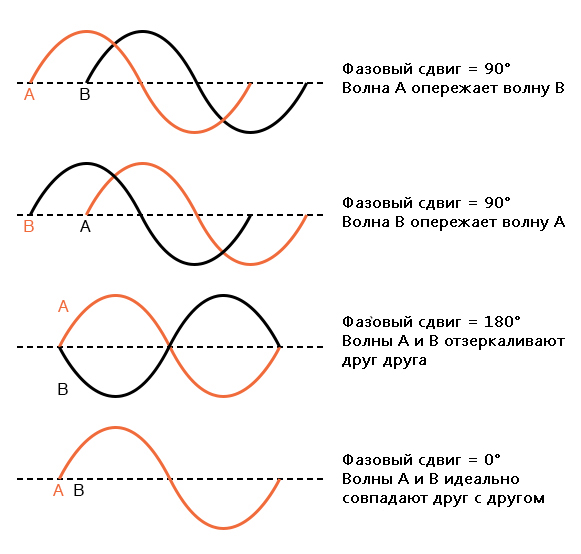
Поскольку формы сигналов в приведённых выше примерах имеют одинаковую частоту, они будут отличаться в каждом шаге на одинаковую угловую величину в каждый момент времени. По этой причине можно выразить фазовый сдвиг для двух или более сигналов одной и той же частоты как постоянную величину для всей волны, а не заново каждый раз вычислять сдвиг между любыми двумя точками вдоль волн.
То есть можно уверенно сказать что-то вроде такого: «Напряжение A сдвинуто по фазе на 45° по сравнению с напряжением В». Тот сигнал, что на графике впереди, называется опережающим, а тот, что позади – отстающим.
Фазовый сдвиг, как и напряжение, всегда является измерением чего-либо в количестве двух (или более чем двух). Т.е., чтобы говорить о фазовом сдвиге, нужно как минимум две волны. На самом деле не существует такой вещи, как форма волны с абсолютной фазой, потому что для фазы нет универсального эталона.
Обычно при анализе цепей переменного тока форма волны для напряжения источника питания используется в качестве эталона для фазы, это напряжение указано как «*** вольт при 0°». Любое другое переменное напряжение или ток в этой цепи будет иметь фазовый сдвиг, выраженный относительно указанного напряжения источника.
Это как раз то, из-за чего расчёты цепей переменного тока более сложны, чем для постоянного тока. При применении закона Ома и правил Кирхгофа величины переменного напряжения и тока должны отражать как фазовый сдвиг, так и амплитуду. Математические операции сложения, вычитания, умножения и деления должны оперировать этими величинами фазового сдвига (и амплитуды).
К счастью, в математике есть комплексные числа, идеально подходящие для задачи одновременного представления в одной переменной и амплитуды и фазы.
Поскольку для понимания цепей переменного тока так важны комплексные числа, в следующей главе мы их рассмотрим подробнее.
Итог
- Фазовый сдвиг – это когда две (или более) формы сигналов (волн) не совпадают друг с другом.
- Величина фазового сдвига между двумя волнами может быть выражена в градусах, если разметить в градусах горизонтальную ось графика формы волны, используемую при построении тригонометрической синусоидальной функции.
- Опережающая волна – это та, которая находится по времени впереди в своей эволюции относительно другой волны. Отстающий сигнал – тот, что идёт позади опережающего. Пример:
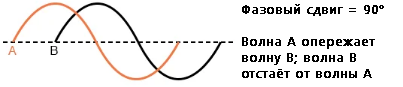
- Точные расчёты для анализа цепей переменного тока предполагают учёт как амплитуды, так и фазового сдвига формы волны для напряжения и тока. Это требует использования специального математического аппарата, известного как комплексные числа.
См.также
Внешние ссылки