Электроника:Переменный ток/Резонанс/Простой последовательный резонанс

Содержание

Теория

Практика

Проверка знаний

Рецепты

Эксперименты

Резерв

Резерв

Резерв

Резерв

Перевод: Макаров В. (valemak)

Проверка/Оформление/Редактирование: Мякишев Е.А.

Простой последовательный резонанс

Аналогичный эффект наблюдается в последовательных индуктивно-ёмкостных цепях. Когда достигается состояние резонанса (ёмкостное и индуктивное реактивные сопротивления равны), два импеданса компенсируют друг друга, и общее сопротивление падает до нуля! Рассмотрим пример:

Рис. 1. Простой последовательный резонансный контур. Ёмкость конденсатора и индуктивность катушки – как и в прошлой параллельной схеме.

Рис. 2. Уравнение простого последовательного резонансного контура. Мы можем воспользоваться значениями реактансов (100 Ом), вычисленные на прошлой лекции.

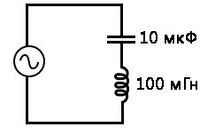
При общем последовательном импедансе, равном 0 Ом на резонансной частоте 159,155 Гц, результатом будет короткое замыкание на источнике питания переменного тока при достижении состояния резонанса. Для нашей последовательной схемы это добром не кончится.

Добавим небольшой резистор (рисунок ниже) последовательно с конденсатором и катушкой индуктивности, чтобы несколько ограничить максимальный ток цепи, и проведем ещё один анализ SPICE в том же диапазоне частот.

Рис. 3. Чтобы избежать короткого замыкания (и тогда мы сможем проанализировать схему в программе SPICE), добавим в последовательный резонансный контур небольшой резистор. Ну, и отметим узловые точки на схеме.

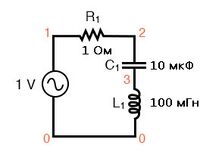
series lc circuit v1 1 0 ac 1 sin r1 1 2 1 c1 2 3 10u l1 3 0 100m .ac lin 20 100 200 .plot ac i(v1) .end

Для этой программы модуль Nutmeg покажет такой график:

Рис. 4. График последовательного резонансного контура относительно силы тока I(v1).

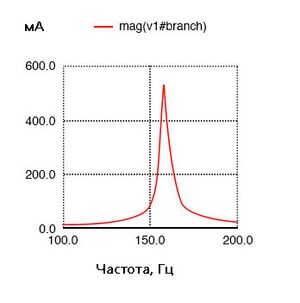
Как и в прошлый раз, по вертикальной оси увеличивается амплитуда силы тока в цепи, а по горизонтальной – частота. Пик по-прежнему находится в отмеченной на графике точке с частотой 157,9 Гц, это ближайшая проанализированная точка к нашей предсказанной точке резонанса 159,155 Гц.

Предполагается, что наша формула резонансной частоты верна как для простых последовательных LC-цепей, так и для простых параллельных LC-цепей:

Рис. 5. Универсальная формула резонансной частоты.

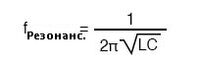
С последовательными резонансными LC-контурами нужно быть предельно осторожными: из-за высоких токов, которые могут быть в этом случае, возможно возникновение опасно высоких падений напряжения на конденсаторе и катушке индуктивности, поскольку каждый компонент обладает значительным импедансом. Слегка отредактируем программу для SPICE, чтобы также в графике показать напряжения на конденсаторе и катушке индуктивности.

series lc circuit v1 1 0 ac 1 sin r1 1 2 1 c1 2 3 10u l1 3 0 100m .ac lin 20 100 200 .plot ac i(v1) v(2,3) v(3) .end

Рис. 6. График напряжения на конденсаторе V_C = v(2,3) имеет пик 70 В; график напряжения на катушке индуктивности V_L = v(3) имеет пик 70 В; график для силы тока I = I(v1#branch) имеет пик 0,532.

SPICE говорит, что напряжение на конденсаторе и катушке индуктивности достигает пика где-то около 70 вольт! Это немало для блока питания, вырабатывающего всего 1 вольт. Так что снова стоит напомнить, что при экспериментировании с подобными схемами следует проявлять повышенную осторожность. Напряжение SPICE ниже ожидаемого значения из-за небольшого (всего лишь 20) количества шагов в операторе анализа переменного тока (.ac lin 20 100 200). А чему равно ожидаемое значение?

Дано: fr = 159.155 Гц, L = 100 мГн, R = 1 Ом XL = 2πfL = 2π(159,155 Гц)(100 мГн) = j100 Ом XC = 1/(2πfC) = 1/(2π(159,155 Гц)(10 мкФ)) = -j100 Ом Z = 1 + j100 - j100 = 1 Ом I = V/Z = (1 В)/(1 Ом) = 1 A VL = IZ = (1 A)(j100 Ом) = j100 В VC = IZ = (1 A)(-j100 Ом) = -j100 В VR = IR = (1 A)(1 Ом)= 1 В VВсего = VL + VC + VR VВсего = j100 - j100 +1 = 1 В

Ожидаемые значения для напряжения конденсатора и катушки индуктивности составляют 100 В. Это напряжение нагружает эти компоненты до такого уровня, поэтому они должны быть рассчитаны соответствующим образом. Однако эти напряжения не совпадают по фазе и нейтрализуют друг друга, в результате чего общее напряжение на всех трёх компонентах составляет всего 1 В – это и есть приложенное напряжение. Отношение напряжения конденсатора (или катушки индуктивности) к приложенному напряжению является фактором «добротности» (о которой мы в этой главе далее поговорим).

Q = VL/VR = VC/VR

Итог

• Общий импеданс последовательной LC-цепи приближается к нулю, когда частота источника питания приближается к резонансной частоте.
• Та же формула для определения резонансной частоты в простом колебательном контуре применима и к простым последовательным LC-цепям.
• На отдельных компонентах последовательных LC-цепей могут формироваться чрезвычайно высокие напряжения. Это может происходить при резонансе из-за большого токового потока и значительного импеданса отдельных компонентов.