Перевод: Макаров В. (valemak)
Проверка/Оформление/Редактирование: Мякишев Е.А.
Практическая коррекция коэффициента мощности[1] Когда нужно исправить низкий коэффициент мощности в системе питания переменного тока, вы, вероятно, будете лишены роскоши знать точную индуктивность нагрузки в генри, чтобы использовать её в своих расчётах.
Возможно, вам повезло иметь прибор, называемый измерителем коэффициента мощности , который сообщит вам, каковы КМ (число от 0 до 1) и полная мощность (которую можно вычислить, сняв показания вольтметра в вольтах и умножив их на показание амперметра в амперах).
Если повезёт меньше, то вам, возможно, придётся использовать осциллограф для сравнения волн напряжения и тока, измерения фазового сдвига в градусах и вычисления коэффициента мощности по косинусу этого фазового сдвига.
Скорее всего, у вас будет доступ к ваттметру для измерения истинной мощности, показания которого вы можете сравнить с расчётом полной мощности (умножением общего напряжения на измерения общего тока). По значениям истинной и полной мощности вы сможете определить реактивную мощность и коэффициент мощности.
Пример проблемы Давайте рассмотрим на примере, как это работает:
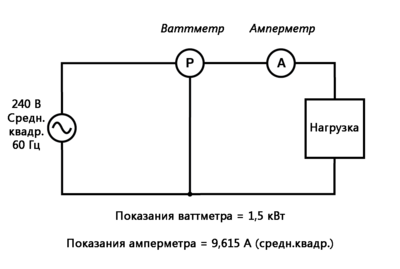
Рис. 1. Ваттметр показывает истинную мощность; произведение показаний вольтметра и амперметра даёт полную мощность.
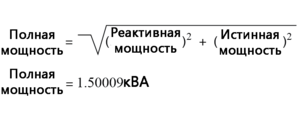
Рассчитываем полную мощность в кВА Во-первых, нам нужно рассчитать полную мощность в кВА. Это можно сделать, умножив напряжение нагрузки на ток нагрузки:
Рис. 2. Расчёт полной мощности Как видим, 2,308 кВА – это намного больше, чем 1,5 кВт, что говорит нам о том, что коэффициент мощности в этой цепи довольно низкий (существенно меньше 1). Теперь мы рассчитаем коэффициент мощности этой нагрузки, разделив истинную мощность на полную:
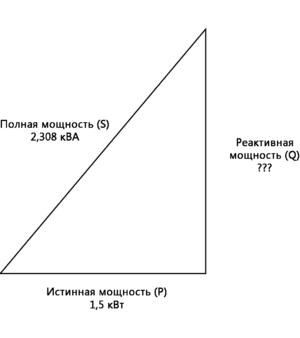
Рис. 3. Вычисляем текущий коэффициент мощности. Используя это значение коэффициента мощности, можно нарисовать треугольник мощности и по нему определить реактивную мощность нагрузки:
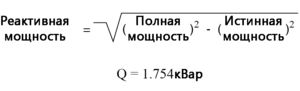
Рис. 4. Реактивная мощность может быть рассчитана на основе истинной мощности и полной мощности. Применяем теорему Пифагора для определения неизвестных величин в прямоугольном треугольнике Чтобы определить неизвестную величину треугольника (катет, изображающий реактивную мощность), используем теорему Пифагора «в обратном направлении», учитывая известную длину гипотенузы (полная мощность) и длину смежной стороны (истинная мощность):
Рис. 5. Зная гипотенузу и один из катетов, по теореме Пифагора находим второй катет. Корректируем коэффициент мощности с помощью конденсатора Если эта нагрузка представляет собой электродвигатель или любую другую промышленную нагрузку переменного тока, она будет иметь запаздывающий (индуктивный) коэффициент мощности, что означает, что нам придётся исправить это с помощью конденсатора соответствующего размера, подключённого параллельно.
Теперь, когда мы знаем количество реактивной мощности (1,754 кВар), мы можем рассчитать размер конденсатора, необходимого для противодействия её влиянию:
Рис. 6. Находим нужную ёмкость корректирующего конденсатора для того, чтобы коэффициент мощности приблизить к единице. Округляя этот ответ до 80 мкФ, можем поместить конденсатор данной ёмкости в схему и вычислить результаты:
Рис. 7. Параллельный конденсатор корректирует запаздывающую (индуктивную) нагрузку. 80 мкФ конденсатор будет иметь ёмкостное сопротивление 33.157 Ом, что даёт ток 7.238 ампер, и соответствующая реактивная мощность равна 1.737 кВар (только для конденсатора). Поскольку ток конденсатора на 180° не совпадает по фазе с индуктивным вкладом нагрузки в потребляемый ток, реактивная мощность конденсатора будет напрямую вычитаться из реактивной мощности нагрузки, в результате чего получим:
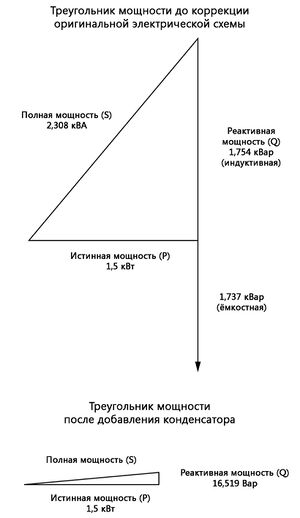
Рис. 8. Вычитание реактивной мощности конденсатора из реактивной мощности нагрузки даст общую мощность. Эта коррекция, конечно, не изменит количество истинной мощности, потребляемой нагрузкой, но приведёт к существенному очевидному снижению мощности и общего тока, потребляемого от источника 240 В:
Рис. 9. Треугольник мощности до и после коррекции с помощью параллельного конденсатора. Новую полную мощность можно найти из новых значений истинной и реактивной мощности, используя стандартную форму теоремы Пифагора:
Рис. 10. Стандартная форма теоремы Пифагора позволяет найти полную мощность (гипотенуза), зная один катет (реактивная мощность) и другой катет (истинная мощность). См.также Внешние ссылки
Партнерские ресурсы Криптовалюты
Магазины
Хостинг
Разное
Викиум - Онлайн-тренажер для мозга Like Центр - Центр поддержки и развития предпринимательства. Gamersbay - лучший магазин по бустингу для World of Warcraft. Ноотропы OmniMind N°1 - Усиливает мозговую активность. Повышает мотивацию. Улучшает память. Санкт-Петербургская школа телевидения - это федеральная сеть образовательных центров, которая имеет филиалы в 37 городах России. Lingualeo.com — интерактивный онлайн-сервис для изучения и практики английского языка в увлекательной игровой форме. Junyschool (Джунискул) – международная школа программирования и дизайна для детей и подростков от 5 до 17 лет, где ученики осваивают компьютерную грамотность, развивают алгоритмическое и креативное мышление, изучают основы программирования и компьютерной графики, создают собственные проекты: игры, сайты, программы, приложения, анимации, 3D-модели, монтируют видео. Умназия - Интерактивные онлайн-курсы и тренажеры для развития мышления детей 6-13 лет SkillBox - это один из лидеров российского рынка онлайн-образования. Среди партнеров Skillbox ведущий разработчик сервисного дизайна AIC, медиа-компания Yoola, первое и самое крупное русскоязычное аналитическое агентство Tagline, онлайн-школа дизайна и иллюстрации Bang! Bang! Education, оператор PR-рынка PACO, студия рисования Draw&Go, агентство performance-маркетинга Ingate, scrum-студия Sibirix, имидж-лаборатория Персона. «Нетология» — это университет по подготовке и дополнительному обучению специалистов в области интернет-маркетинга, управления проектами и продуктами, дизайна, Data Science и разработки. В рамках Нетологии студенты получают ценные теоретические знания от лучших экспертов Рунета, выполняют практические задания на отработку полученных навыков, общаются с экспертами и единомышленниками. Познакомиться со всеми продуктами подробнее можно на сайте https://netology.ru, линейка курсов и профессий постоянно обновляется. StudyBay Brazil – это онлайн биржа для португалоговорящих студентов и авторов! Студент получает уникальную работу любого уровня сложности и больше свободного времени, в то время как у автора появляется дополнительный заработок и бесценный опыт. Автор24 — самая большая в России площадка по написанию учебных работ: контрольные и курсовые работы, дипломы, рефераты, решение задач, отчеты по практике, а так же любой другой вид работы. Сервис сотрудничает с более 70 000 авторов. Более 1 000 000 работ уже выполнено. StudyBay – это онлайн биржа для англоязычных студентов и авторов! Студент получает уникальную работу любого уровня сложности и больше свободного времени, в то время как у автора появляется дополнительный заработок и бесценный опыт.
Теория по электронике Постоянный ток Основные концепты электричества
• Статическое электричество Проводники, диэлектрики и поток электронов Что такое электрические цепи Напряжение и электроток Сопротивление Напряжение и электроток в реальной цепи Условный ток и поток электронов Закон Ома
• Закон Ома – Как напряжение, сила тока и сопротивление связаны друг с другом Аналогия для закона Ома Мощность в электрических цепях Расчёт электрической мощности Резисторы Нелинейная проводимость Построение цепи Полярность перепада напряжения Компьютерная симуляция электрических цепей Правила электробезопасности
• Важность правил электробезопасности Воздействие электричества на психологическое состояние Путь, который ток проходит перед ударом Закон Ома (снова!) Техника безопасности Первая медицинская помощь при ударе током Распространённые источники опасности Проектирование электроцепей с учётом требований безопасности Безопасное использование приборов для измерения электрических показателей Данные о влиянии удара током на тело человека Экспоненциальная запись и метрические приставки
• Экспоненциальная запись Арифметические операции для экспоненциальной записи Метрические обозначения Преобразование метрических приставок Используем ручной калькулятор Экспоненциальная форма в программе SPICE Последовательные и параллельные электрические цепи
• Что такое «последовательные» и «параллельные» электрические цепи Простая последовательная цепь Простая параллельная цепь Электропроводность Рассчитываем мощность Правильно используем закон Ома Анализ отказов компонентов цепи Строим простые резистивные цепи Схемы с делителями напряжения и правила Кирхгофа
• Схемы с делителем напряжения Правило напряжений Кирхгофа (ПНК) Цепи – делители тока и формула делителя тока Правило Кирхгофа для силы тока (ПКТ) Комбинированные последовательно-параллельные схемы
• Что такое последовательно-параллельная цепь Методы анализа последовательно-параллельных резисторных цепей Перерисовываем избыточно усложнённые схемы Анализ отказов компонентов (продолжение) Построение простых резисторных цепей Измерения в электрических цепях постоянного тока
• Что такое измеритель? Как устроен вольтметр Как вольтметр влияет на измеряемую цепь Как устроен амперметр Как амперметр влияет на измеряемую цепь Как устроен омметр Высоковольтный омметр Мультиметры Кельвиновское 4-проводное измерение сопротивления Мостовые схемы Как устроен ваттметр Как самостоятельно сделать ручной калибратор Сигналы электрического оборудования
• Аналоговые и цифровые сигналы Системы сигналов напряжения Системы сигналов силы тока Тахогенераторы Теромопары Измерения pH Тензодатчики Анализ сети постоянного тока
• Что такое сетевой анализ? Метод токов ветвей Аналитический метод контурных токов Метод узловых потенциалов Введение в сетевые теоремы Теорема Миллмана Теорема о суперпозиции Теорема Тевенена Теорема Нортона Эквивалентность схем Тевенена и Нортона И вновь о теореме Миллмана Теорема о передаче максимальной мощности Δ-Y и Y-Δ преобразования Батареи и системы питания
• Поведение электронов при химических реакциях Батарейные конструкции Рейтинг батарей Батареи специального назначения Практические рекомендации при использовании батарей Физика проводников и диэлектриков
• Введение в физику проводников и диэлектриков Размеры проводов Допустимые токовые нагрузки на провода Предохранители Удельное сопротивление Температурный коэффициент сопротивления Сверхпроводимость Пробивное напряжение диэлектрика Конденсаторы
• Электрическое поле и ёмкость Конденсаторы и дифференциальное исчисление Факторы, влияющие на ёмкость конденсатора Последовательное и параллельное соединение конденсаторов Практические соображения - Конденсаторы Магнетизм и электромагнетизм
• Постоянные магниты Электромангетизм Единицы измерения магнитных величин Магнитная проницаемость и насыщение Электромагнитная индукция Взаимная индукция Катушки индуктивности
• Магнитные поля и индуктивность Катушки индуктивности и дифференциальное исчисление Факторы, влияющие на индуктивность Катушки индуктивности в последовательных и параллельных соединениях Практические соображения – Катушки индуктивности Постоянные времени в RC и L/R цепях
• Переходные процессы в электрических цепях Переходные процессы в цепях с конденсатором Переходные процессы в цепях с катушкой индуктивности Расчёт напряжения и силы тока Почему L/R, а не LR? Комплексные расчёты напряжения и тока Сложные схемы Расчёт неизвестного времени Переменный ток Основы теории переменного тока
• Что такое переменный ток? Формы волн переменного тока Измерение величин переменного тока Расчёт простейшей цепи переменного тока Фаза переменного тока Принципы радио Комплексные числа
• Введение в комплексные числа Векторы и волны переменного тока Сложение простых векторов Сложение сложных векторов Полярная и алгебраическая запись комплексных чисел Арифметика комплексных чисел И ещё по поводу полярности переменного тока Несколько примеров с цепями переменного тока Реактанс и импеданс – Индуктивность
• Резистор в цепи переменного тока (Индуктивность) Катушка индуктивности в цепи переменного тока Последовательные резистивно-индуктивные цепи Параллельные резистивно-индуктивные цепи Особенности катушек индуктивности Что такое «скин-эффект»? Реактанс и импеданс – Ёмкость
• Резистор в цепи переменного тока (Ёмкость) Конденсатор в цепи переменного тока Последовательные резистивно-ёмкостные цепи Параллельные резистивно-ёмкостные цепи Особенности конденсаторов Реактанс и импеданс – R/L/C-цепи
• Обзор R, X и Z (сопротивление, реактанс и импеданс) Последовательные R/L/C-цепи Параллельные R/L/C-цепи Последовательно-параллельные R/L/C-цепи Реактивная проводимость и адмиттанс R/L/C-цепи – что в итоге? Резонанс
• Электрический маятник Простой параллельный резонанс (колебательный контур) Простой последовательный резонанс Применение резонанса Резонанс в последовательно-параллельных цепях Добротность и полоса пропускания резонансной цепи Сигналы переменного тока смешанной частоты
• Сигналы переменного тока смешанной частоты - Введение Прямоугольные волновые сигналы Другие волновые формы Подробнее о спектральном анализе Эффекты в электрических цепях Фильтры
• Что такое фильтр? Низкочастотные фильтры Высокочастотные фильтры Полосовые фильтры Полосно-заграждающие фильтры Резонансные фильтры Подводя итоги по фильтрам Трансформаторы
• Взаимная индуктивность и основные операции Повышающие и понижающие трансформаторы Электрическая изоляция Фазировка Конфигурации обмотки Регулировка напряжения Специальные трансформаторы и приложения Практические соображения – Трансформаторы Многофазные цепи переменного тока
• Однофазные системы питания Трёхфазные системы питания Чередование фаз Устройство многофазного двигателя Трёхфазные Y- и дельта-конфигурации Трёхфазные цепи с трансформатором Гармоники в многофазных энергосистемах Гармонические фазовые последовательности Коэффициент мощности
• Мощность в резистивных и реактивных цепях переменного тока Истинная, реактивная и полная мощность Расчёт коэффициента мощности Практическая коррекция коэффициента мощности Измерение цепей переменного тока
• Вольтметры и амперметры переменного тока Измерение частоты и фазы Измерение мощности Измерение качества электроэнергии Мостовые схемы переменного тока Измерительные преобразователи переменного тока Двигатели переменного тока
• Введение в двигатели переменного тока Синхронные двигатели Синхронный конденсатор Двигатель с магнитным сопротивлением Шаговые двигатели Бесщёточный двигатель постоянного тока Многофазные асинхронные двигатели Теслы Асинхронные двигатели с фазным ротором Однофазные асинхронные двигатели Прочие специализированные двигатели Сельсин-двигатели (синхронизированные двигатели) Коллекторные двигатели переменного тока Линии передачи
• Кабель на 50 Ом? Электрические цепи и скорость света Характеристический импеданс Линии передачи конечной длины «Длинные» и «короткие» линии передачи Стоячие волны и резонанс Преобразование импеданса Волноводы Полупроводники Усилители и активные устройства
• От электрики к электронике Активные и пассивные устройства Усилители Коэффициент усиления Децибелы Абсолютные дБ-шкалы Аттенюаторы Теория твердотельных приборов
• Введение в теорию твердотельных устройств Квантовая физика Валентность и кристаллическая структура Зонная теория твёрдых тел Электроны и «дырки» P-N-переход Полупроводниковые диоды Транзисторы с биполярным переходом Полевые транзисторы Полевые транзисторы с изолированным затвором (MOSFET) Тиристоры Методы производства полупроводников Сверхпроводящие устройства Квантовые устройства Полупроводниковые приборы в SPICE Диоды и выпрямители
• Диоды и выпрямители – Введение Проверка диодов мультиметром Номинальные характеристики диодов Схемы выпрямителей Пиковый детектор Схемы ограничителей напряжения Схемы фиксаторов уровня Умножители напряжения (удвоители, утроители, учетверители и т.д.) Схемы коммутации индуктивных нагрузок Диодные схемы коммутации Что такое диод Зенера (стабилитрон)? Диоды специального назначения Прочие диодные технологии Модели диодов в SPICE Биполярные транзисторы
• Транзисторы с биполярным переходом (ТБП) – Введение Транзистор с биполярным переходом (ТБП) как переключатель Проверка транзистора с биполярным переходом (ТБП) с помощью мультиметра Активный режим работы транзистора с биполярным переходом (ТБП) Усилительный каскад с общим эмиттером Усилительный каскад с общим коллектором Усилительный каскад с общей базой Каскодный усилитель Методы смещения для транзисторов с биполярным переходом (ТБП) Расчёт смещения для транзисторов с биполярным переходом (ТБП) Взаимодействие входа и выхода в транзисторах с биполярным переходом (ТБП) Обратная связь в транзисторах с биполярным переходом (ТБП) Импеданс усилителя Токовые зеркала в транзисторах с биполярным переходом (ТБП) Параметры и корпуса транзисторов с биполярным переходом (ТБП) Особенности транзисторов с биполярным переходом (ТБП) Полевые транзисторы
• Полевые транзисторы (JFET) – Введение Полевой транзистор (JFET) как переключатель Проверка полевого транзистора (JFET) с помощью мультиметра Активный режим работы полевого транзистора (JFET) Полевые транзисторы с изолированным затвором
• Полевые транзисторы с изолированным затвором – Введение Обедняющие полевые транзисторы с изолированным затвором Биполярные транзисторы с изолированным затвором Тиристоры
• Гистерезис Газоразрядные лампы Диод Шокли (динистор) DIAC (симметричный динистор) Управляемый кремниевый выпрямитель (SCR-тиристор) TRIAC (симметричный тринистор, триак) Оптотиристоры Однопереходной транзистор Управляемый кремниевый коммутатор (SCS-тиристор) Тиристоры с полевым управлением Операционные усилители
• Операционные усилители (ОУ) – Введение Несимметричные и дифференциальные усилители «Операционный» усилитель Отрицательная обратная связь Делитель напряжения в цепи обратной связи Аналогия для делителя напряжения в цепи обратной связи Преобразование сигнала напряжения в сигнал тока Схемы усреднителя и сумматора Построение дифференциальных усилителей Инструментальный (измерительный) усилитель Схемы дифференциатора и интегратора Положительная обратная связь Практические аспекты ОУ Модели операционных усилителей Практические аналоговые полупроводниковые схемы
• Электростатический разряд Схемы источников питания Схемы усилителей Осцилляторные схемы Радиосхемы Вычислительные схемы Измерительные схемы Приводы двигателей постоянного тока
• Широтно-импульсная модуляция Электронные лампы
• Электронные лампы – Введение История электронных ламп – с чего всё началось Триод Тетрод Силовой лучевой тетрод Пентод Комбинированные электронные лампы Характеристики электронных ламп Ионизированные (газовые) электронные лампы Индикаторные электронные лампы Микроволновые электронные лампы Сравниваем электронные лампы и полупроводники Цифровая электроника Системы счисления
• Числа и способы их выражения Системы счисления Сравниваем десятеричные и двоичные числа Восьмеричная и шестнадцатеричная системы счисления Восьмеричные и шестнадцатеричные числа преобразовываем в десятеричные Преобразование из десятеричной системы счисления Двоичная арифметика
• Числа и системы счисления Двоичное сложение Отрицательные двоичные числа Двоичное вычитание Двоичное переполнение Наборы битов Логические вентили
• Цифровые сигналы и вентили Вентили «НЕ» «Буферные» вентили Вентили с более чем одним входом Транзисторно-транзисторная логика вентилей «И-НЕ» и «И» Транзисторно-транзисторная логика вентилей «ИЛИ-НЕ» и «ИЛИ» Схемы КМОП-вентилей Специальные выходы в вентилях Универсальность вентилей «И-НЕ» и «ИЛИ-НЕ» Уровни напряжения для «высоких» и «низких» логических сигналов Вентильные DIP корпусы Переключатели
• Типы переключателей Как устроены контакты переключателей «Нормальное» состояние контакта и последовательное замыкание/размыкание «Дребезжание» контактов Электромеханические реле
• Устройство реле Контакторы Реле с задержкой времени Защитные реле Твердотельные реле Релейная логика
• «Лестничные» диаграммы Функции цифровой логики Разрешающие и блокирующие схемы Схемы управления двигателем Отказоустойчивость Программируемые логические контроллеры (ПЛК) Булева алгебра
• Булева алгебра – Введение Логическая арифметика Булевы алгебраические тождества Булевы алгебраические свойства Логические правила для упрощения Примеры упрощения схем Функция «Исключающее ИЛИ»: вентиль XOR Законы де Моргана Преобразование таблиц истинности в логические выражения Карты Карно
• Карты Карно – Введение Диаграммы Венна и множества Булевы соотношения на диаграммах Венна Преобразование диаграмм Венна в карты Карно Карты Карно, таблицы истинности и логические выражения Упрощение логики с помощью карт Карно Бо́льшие карты Карно с 4-мя переменными Минтермы и макстермы в реализациях Обозначения сумм и произведений Поля «безразличия» на картах Карно Бо́льшие карты Карно с 5-ю и 6-ю переменными Функции комбинационной логики
• Функции комбинационной логики – Введение Неполный сумматор Полный сумматор Декодер Кодер Демультиплексоры Мультиплексоры Совместное использование множественных комбинационных схем Мультивибраторы
• Цифровая логика с обратной связью SR-защёлка Вентильная SR-защёлка D-защёлка Защёлки с запуском по фронту сигнала: триггеры JK-триггер Триггеры с асинхронными входами Моностабильные мультивибраторы Схемы последовательностей
• Двоичная счётная последовательность Асинхронные счётчики Синхронные счётчики Конечные автоматы Сдвиговые регистры
• Сдвиговые регистры – Введение Сдвиговые регистры: последовательный вход, последовательный выход (SISO) Сдвиговые регистры: параллельный вход, последовательный выход (PISO) Сдвиговые регистры: последовательный вход, параллельный выход (SIPO) Универсальные сдвиговые регистры: параллельный вход, параллельный выход (PIPO) Кольцевые счётчики Цифро-аналоговые и аналого-цифровые преобразования
• Цифро-аналоговые (ЦАП) и аналого-цифровые (АЦП) преобразования – Введение ЦАП R/2nR: цифро-аналоговый преобразователь с двоично-взвешенным входом ЦАП R/2R: (цифро-аналоговый преобразователь) Параллельные АЦП Цифровые ступенчатые АЦП АЦП с последовательным приближением Отслеживающий АЦП Скатные (интегрирующие) АЦП Дельта-сигма АЦП Практические аспекты схем АЦП Цифровая связь
• Цифровая связь – Введение Сети и шины Потоки данных Типы электрических сигналов Оптическая передача данных Топология сети Сетевые протоколы Практические аспекты цифровой связи Цифровое хранилище (память)
• Почему «цифровое»? Понятия и концепции цифровой памяти Современная немеханическая память Устаревшие немеханические технологии памяти Постоянное запоминающее устройство (ПЗУ) Память с движущимися частями: «Приводы» Принципы цифровых вычислений
• Двоичный сумматор Таблицы поиска Конечные автоматы Микропроцессоры Микропроцессорное программирование Справочные материалы Полезные уравнения и коэффициенты пересчёта
• Уравнения и законы для цепей постоянного тока Правила последовательных цепей Правила параллельных цепей Эквивалентные значения компонентов в последовательных и параллельных цепях Уравнение ёмкости конденсатора Уравнение катушки индуктивности Уравнения постоянной времени Уравнения цепей переменного тока Уравнения для децибел Метрические приставки и преобразования единиц измерения Цветовая маркировка
• Цветовая маркировка резисторов Цветовая маркировка проводки Инфографика цветовой маркировки проводки Таблицы проводников и диэлектриков
• Таблица калибров медной проволоки Таблица допустимых нагрузок для медного провода Коэффициенты удельного сопротивления Таблица температурных коэффициентов сопротивления Критические температуры для сверхпроводников Диэлектрическая прочность изоляторов Справочник по алгебре
• Основные алгебраические тождества Основные свойства арифметики Свойства степеней Извлечение корней Важные константы Логарифмы Формулы сокращённого умножения Квадратное уравнение Прогрессии Факториалы Решение систем уравнений: метод подстановки и метод сложения Справочник по тригонометрии
• Тригонометрия прямоугольного треугольника Тригонометрия произвольного треугольника Тригонометрические формулы Гиперболические функции Справочник по исчислению
• Формулы вычисления пределов Производная числа Общие производные Производные показательных функций с основанием e Производные простых тригонометрических функций Правила вычисления производных Первообразная (неопределённый интеграл) Общие первообразные Первообразные показательных функций от числа e Правила вычисления первообразных Определённые интегралы и основная теорема исчисления Дифференциальные уравнения Использование программы SPICE для моделирования электрических схем
• Программа моделирования электрических цепей SPICE — Введение История программы SPICE Основы программирования в SPICE Интерфейс командной строки Компоненты электрических схем Опции для проведения анализа Странные особенности программы SPICE Примеры электрических цепей и списков связей Устранение неполадок – теория и практика
• Вопросы, которые следует задать, прежде чем продолжить Общие советы по устранению неполадок Конкретные методы устранения неполадок Вероятные сбои в проверенных системах Вероятные сбои в непроверенных системах Возможные ментальные ловушки Схематические обозначения элементов цепи
• Провода и соединения Источники питания Типы резисторов Типы конденсаторов Катушки индуктивности Взаимные катушки индуктивности Переключатели с ручным управлением Управляемые процессом переключатели Переключатели с электрическим приводом (реле) Соединители Диоды Биполярные транзисторы Переходные транзисторы с полевым эффектом (JFET) Транзисторы с полевым эффектом с изолированным затвором (IGFET или MOSFET) Гибридные транзисторы Тиристоры Интегральные схемы Электронные лампы Периодическая таблица химических элементов
• Таблица Менделеева Эксперименты Введение
• Электроника как точная наука Обустраиваем домашнюю лабораторию Основные концепции и испытательное оборудование
• Использование вольтметра Использование омметра Очень простая схема Использование амперметра при измерении силы тока Закон Ома Нелинейное сопротивление Рассеяние мощности Цепь с переключателем Эксперимент по электромагнетизму Эксперимент с электромагнитной индукцией Электрические цепи постоянного тока
• Электрические цепи постоянного тока – Введение Последовательные источники питания Параллельные источники питания Делитель напряжения Делитель тока Потенциометр как делитель напряжения Потенциометр как реостат Прецизионный потенциометр Ограничение диапазона реостата Термоэлектричество Мультиметр своими руками Чувствительный детектор напряжения Потенциометрический вольтметр 4-проводное измерение сопротивления Простейший компьютер Картошка-батарейка Зарядка и разрядка конденсатора Индикатор скорости изменения Электрические цепи переменного тока
• Электрические цепи переменного тока – Введение Трансформатор – блок питания Сборка трансформатора Переменный индуктор Чувствительный аудиодетектор Обнаружение магнитных полей переменного тока Обнаружение электрических полей переменного тока Альтернатор – автомобильный генератор Асинхронный двигатель Асинхронный двигатель побольше Фазовый сдвиг Погашение звука Музыкальный синтезатор как генератор сигналов ПК-осциллограф Анализ волновых сигналов Колебательный контур Сигнальная связь Дискретные полупроводниковые схемы
• Дискретные полупроводниковые схемы – Введение Коммутирующий диод Полупериодный выпрямитель Двухполупериодный мостовой выпрямитель Двухполупериодный выпрямитель с центральным отводом Цепь «выпрямитель/фильтр» Регулятор напряжения Транзистор как переключатель Датчик статического электричества Датчик импульсного света Повторитель напряжения Усилитель с общим эмиттером Многокаскадный усилитель Как построить схему токового зеркала JFET – регулятор тока Дифференциальный усилитель Простой операционный усилитель Аудио осциллограф Ламповый аудио усилитель Аналоговые интегральные схемы
• Аналоговые интегральные схемы – Введение Компаратор напряжения Прецизионный повторитель напряжения Неинвертирующий усилитель Высокоимпедансный вольтметр Интегратор Аудио осциллограф на таймерной схеме 555 Наклонный генератор на таймерной схеме 555 ШИМ-контроллер мощности Аудиоусилитель класса B Цифровые интегральные схемы
• Цифровые интегральные схемы – Введение Основная функция вентилей SR-защёлка на основе вентилей «ИЛИ-НЕ» SR-защёлка на основе вентиля «И-НЕ» с входом разрешения SR-триггер на основе вентиля «И-НЕ» Светодиодный секвенсор Простейший кодовый замок 3-битный двоичный счётчик 7-сегментный дисплей Таймерные схемы 555
• Интегральный таймер 555 Триггер Шмитта на интегральном таймере 555 Гистерезисный осциллограф на интегральном таймере 555 Моностабильный мультивибратор на интегральном таймере 555 Минимальное количество комплектующих для КМОП-схемы 555 проблескового прибора длительного действия на красных светодиодах КМОП-схема 555 проблескового прибора длительного действия на синих светодиодах КМОП-схема 555 проблескового прибора длительного действия на светодиодах обратного хода КМОП-схема 555 проблескового прибора длительного действия на красных светодиодах