Электроника:Цифровая электроника/Булева алгебра/Булевы алгебраические свойства: различия между версиями
Valemak (обсуждение | вклад) (Новая страница: «{{Панель управления/Электроника}} {{Перевод от valemak}} {{Myagkij-редактор}} =Булевы алгебраическ...») |
Нет описания правки |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 13: | Строка 13: | ||
По сути, свойство коммутативности сообщает нам, что мы можем изменить порядок переменных (складываемых либо умножаемых) и это не повлияет на истинность выражения: | По сути, свойство коммутативности сообщает нам, что мы можем изменить порядок переменных (складываемых либо умножаемых) и это не повлияет на истинность выражения: | ||
{| class="wikitable" | {| class="wikitable" style="margin:0 auto" | ||
|- | |- | ||
| [[File:IV-7_4_1_1.png|400px|center|thumb|'''Рис. 1.1.''' Если изменить порядок складываемых логических величин, то на величину всего выражения это не повлияет.|alt=Рис. 1.1. Если изменить порядок складываемых логических величин, то на величину всего выражения это не повлияет.]] || [[File:IV-7_4_1_2.png|400px|center|thumb|'''Рис. 1.2.''' Если изменить порядок перемножаемых логических величин, то на величину всего выражения это не повлияет.|alt=Рис. 1.2. Если изменить порядок перемножаемых логических величин, то на величину всего выражения это не повлияет.]] | | [[File:IV-7_4_1_1.png|400px|center|thumb|'''Рис. 1.1.''' Если изменить порядок складываемых логических величин, то на величину всего выражения это не повлияет.|alt=Рис. 1.1. Если изменить порядок складываемых логических величин, то на величину всего выражения это не повлияет.]] || [[File:IV-7_4_1_2.png|400px|center|thumb|'''Рис. 1.2.''' Если изменить порядок перемножаемых логических величин, то на величину всего выражения это не повлияет.|alt=Рис. 1.2. Если изменить порядок перемножаемых логических величин, то на величину всего выражения это не повлияет.]] | ||
| Строка 24: | Строка 24: | ||
Это свойство гласит, что мы можем группировать складываемые/перемножаемые переменные с помощью скобок, и это не изменит истинность всего уравнения. | Это свойство гласит, что мы можем группировать складываемые/перемножаемые переменные с помощью скобок, и это не изменит истинность всего уравнения. | ||
{| class="wikitable" | {| class="wikitable" style="margin:0 auto" | ||
|- | |- | ||
| [[File:IV-7_4_2_1.png|400px|center|thumb|'''Рис. 2.1.''' Можно в каком угодно порядке складывать логические величины – на итоговый результат это не повлияет.|alt=Рис. 2.1. Можно в каком угодно порядке складывать логические величины – на итоговый результат это не повлияет.]] || [[File:IV-7_4_2_2.png|400px|center|thumb|'''Рис. 2.2.''' Можно в каком угодно порядке перемножать логические величины – на итоговый результат это не повлияет.|alt=Рис. 2.2. Можно в каком угодно порядке перемножать логические величины – на итоговый результат это не повлияет.]] | | [[File:IV-7_4_2_1.png|400px|center|thumb|'''Рис. 2.1.''' Можно в каком угодно порядке складывать логические величины – на итоговый результат это не повлияет.|alt=Рис. 2.1. Можно в каком угодно порядке складывать логические величины – на итоговый результат это не повлияет.]] || [[File:IV-7_4_2_2.png|400px|center|thumb|'''Рис. 2.2.''' Можно в каком угодно порядке перемножать логические величины – на итоговый результат это не повлияет.|alt=Рис. 2.2. Можно в каком угодно порядке перемножать логические величины – на итоговый результат это не повлияет.]] | ||
| Строка 42: | Строка 42: | ||
=См.также= | =См.также= | ||
=Внешние ссылки= | =Внешние ссылки= | ||
| Строка 48: | Строка 48: | ||
<references /> | <references /> | ||
{{Навигационная таблица/Электроника | {{Навигационная таблица/Портал/Электроника}} | ||
Текущая версия от 21:51, 22 мая 2023
Булевы алгебраические свойства[1]
Другой тип математических тождеств, называемый «свойствами» или «законами», описывает, как различные переменные соотносятся друг с другом в числовой системе.
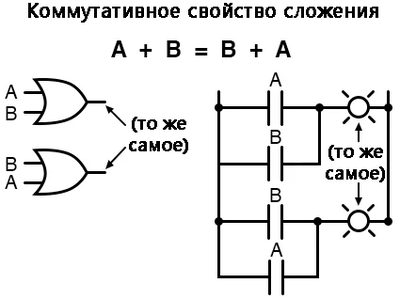
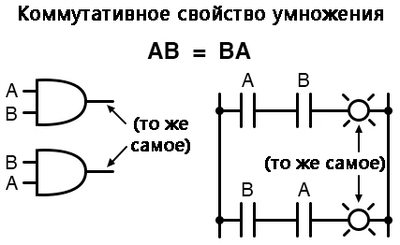
Свойство коммутативности
Одно из этих свойств известно как свойство коммутативности, и оно в одинаковой степени применимо как к сложению, так и к умножению.
По сути, свойство коммутативности сообщает нам, что мы можем изменить порядок переменных (складываемых либо умножаемых) и это не повлияет на истинность выражения:
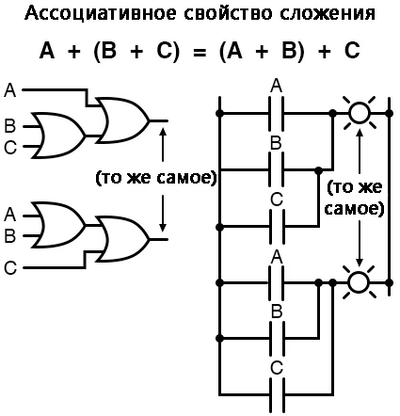
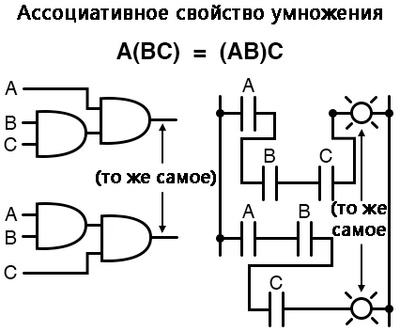
Свойство ассоциативности
Наряду со свойствами коммутативности для сложения и умножения, есть ещё свойство ассоциативности, которое одинаково хорошо применимо и к сложению, и к умножению.
Это свойство гласит, что мы можем группировать складываемые/перемножаемые переменные с помощью скобок, и это не изменит истинность всего уравнения.
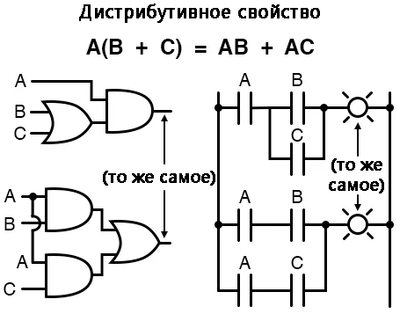
Свойство дистрибутивности
И наконец, у нас есть свойство дистрибутивности, показывающее, как развернуть логическое выражение, образованное произведением суммы, и наоборот, как величины могут быть выведены из логических сумм произведений:
Итог
Подытожим: в булевой алгебре есть три основных свойства: коммутативное, ассоциативное и дистрибутивное.

См.также
Внешние ссылки