Электроника:Переменный ток/Многофазные цепи переменного тока/Гармонические фазовые последовательности: различия между версиями
Myagkij (обсуждение | вклад) (Новая страница: «{{Панель управления/Электроника}} {{Перевод от valemak}} {{Myagkij-редактор}} =<ref>[ www.allaboutcircuits.com - ]</r...») |
Нет описания правки |
||
| (не показаны 3 промежуточные версии 2 участников) | |||
| Строка 3: | Строка 3: | ||
{{Myagkij-редактор}} | {{Myagkij-редактор}} | ||
=<ref>[ www.allaboutcircuits.com - ]</ref>= | =Гармонические фазовые последовательности<ref>[https://www.allaboutcircuits.com/textbook/alternating-current/chpt-10/harmonic-phase-sequences/ www.allaboutcircuits.com - Harmonic Phase Sequences ]</ref>= | ||
В последнем разделе мы увидели, как 3-я гармоника и все её целые кратные (вместе называемые тройными гармониками), генерируемые фундаментальными сигналами, сдвинутыми по фазе на 120°, на самом деле находятся в фазе друг с другом. | |||
В трёхфазной энергосистеме с частотой 60 Гц, где фазы '''A''', '''B''' и '''C''' разнесены на 120°, гармоники, кратные третьей для этих частот (180 Гц) идеально совпадают по фазе друг с другом. | |||
Это можно представить и в графическом виде, и в математических терминах: | |||
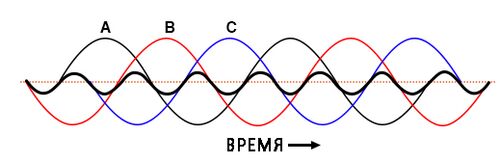
[[File:II-10_8-1.jpg|500px|center|thumb|Рис. 1. Гармонические токи фаз A, B, C совпадают, то есть чередования нет.]] | |||
[[File:II-10_8-2.jpg|400px|center|thumb|Рис. 2. Расширенная математическая таблица с нечётными гармониками.]] | |||
{{ads2}} | |||
Если мы расширим математическую таблицу, включив в неё нечётные гармоники более высоких порядков, то заметим интересную закономерность в отношении чередования или последовательности гармонических частот: | |||
[[File:II-10_8-3.jpg|500px|center|thumb|Рис. 3. Чередование или последовательность гармонических частот.]] | |||
Такие гармоники, как седьмая, «чередуются» в той же последовательности, что и основная гармоника, составляют так называемую ''положительную последовательность''. | |||
Такие гармоники, как пятая, «чередуются» в последовательности, противоположной основной, которые составляют так называемую ''отрицательную последовательность''. | |||
Тройные гармоники (например, 3-я и 9-я, показанные в этой таблице), которые вообще не «чередуются», потому что находятся в фазе друг с другом, составляют так называемую ''нулевую последовательность''. | |||
Этот паттерн «положительный-нулевой-отрицательный-положительный» продолжается бесконечно для всех нечётных гармоник, что можно представить в виде такой таблицы: | |||
[[File:II-10_8-4.jpg|650px|center|thumb|Рис. 4. Последовательность чередования (положительная, нулевая или отрицательная) в соответствии с порядковым номером гармоники (гармоническим числом).]] | |||
=См.также= | =См.также= | ||
=Внешние ссылки= | =Внешние ссылки= | ||
| Строка 16: | Строка 39: | ||
<references /> | <references /> | ||
{{Навигационная таблица/Электроника | {{Навигационная таблица/Портал/Электроника}} | ||
Текущая версия от 21:41, 22 мая 2023
Гармонические фазовые последовательности[1]
В последнем разделе мы увидели, как 3-я гармоника и все её целые кратные (вместе называемые тройными гармониками), генерируемые фундаментальными сигналами, сдвинутыми по фазе на 120°, на самом деле находятся в фазе друг с другом.
В трёхфазной энергосистеме с частотой 60 Гц, где фазы A, B и C разнесены на 120°, гармоники, кратные третьей для этих частот (180 Гц) идеально совпадают по фазе друг с другом.
Это можно представить и в графическом виде, и в математических терминах:
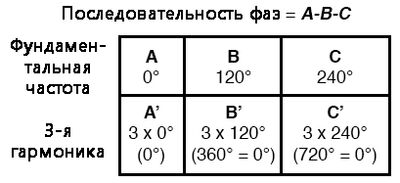
Если мы расширим математическую таблицу, включив в неё нечётные гармоники более высоких порядков, то заметим интересную закономерность в отношении чередования или последовательности гармонических частот:
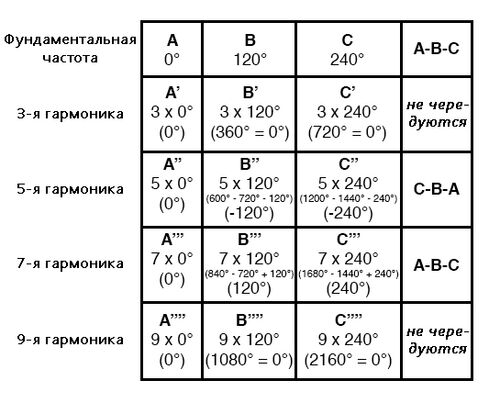
Такие гармоники, как седьмая, «чередуются» в той же последовательности, что и основная гармоника, составляют так называемую положительную последовательность.
Такие гармоники, как пятая, «чередуются» в последовательности, противоположной основной, которые составляют так называемую отрицательную последовательность.
Тройные гармоники (например, 3-я и 9-я, показанные в этой таблице), которые вообще не «чередуются», потому что находятся в фазе друг с другом, составляют так называемую нулевую последовательность.
Этот паттерн «положительный-нулевой-отрицательный-положительный» продолжается бесконечно для всех нечётных гармоник, что можно представить в виде такой таблицы:

См.также
Внешние ссылки