Электроника:Переменный ток/Реактанс и импеданс – Индуктивность/Последовательные резистивно-индуктивные цепи: различия между версиями
Valemak (обсуждение | вклад) Нет описания правки |
Myagkij (обсуждение | вклад) Нет описания правки |
||
| Строка 11: | Строка 11: | ||
Возьмем такую схему в качестве первого примера: | Возьмем такую схему в качестве первого примера: | ||
[[File:Пример последовательной схемы «резистор-индуктор»_1_09062021_0948.png|frame|center|Рис. 1. Пример последовательной схемы «резистор-индуктор».]] | [[File:Пример последовательной схемы «резистор-индуктор»_1_09062021_0948.png|frame|center|Рис. 1. Пример последовательной схемы «резистор-индуктор».|alt=Рис. 1. Пример последовательной схемы «резистор-индуктор».]] | ||
В индуктивной цепи, в которой помимо катушки есть последовательный резистор, волна тока будет отставать от волны приложенного напряжения в пределах от 0° до 90°. | В индуктивной цепи, в которой помимо катушки есть последовательный резистор, волна тока будет отставать от волны приложенного напряжения в пределах от 0° до 90°. | ||
| Строка 22: | Строка 22: | ||
Этот термин называется импедансом, обозначается буквой «Z». Выражается в единицах «Ом», точно так же, как простое сопротивление и реактивное сопротивление. В приведённом выше примере полное сопротивление цепи составляет: | Этот термин называется импедансом, обозначается буквой «Z». Выражается в единицах «Ом», точно так же, как простое сопротивление и реактивное сопротивление. В приведённом выше примере полное сопротивление цепи составляет: | ||
[[File:Расчёт полного сопротивления (импеданса) цепи_2_09062021_0949.jpg|frame|center|Рис. 2. Расчёт полного сопротивления (импеданса) цепи.]] | [[File:Расчёт полного сопротивления (импеданса) цепи_2_09062021_0949.jpg|frame|center|Рис. 2. Расчёт полного сопротивления (импеданса) цепи.|alt=Рис. 2. Расчёт полного сопротивления (импеданса) цепи.]] | ||
== Сопротивление в соответствии с законом Ома == | == Сопротивление в соответствии с законом Ома == | ||
| Строка 28: | Строка 28: | ||
Импеданс ожидаемо связан по закону Ома с напряжением и током аналогично обычному сопротивлению: | Импеданс ожидаемо связан по закону Ома с напряжением и током аналогично обычному сопротивлению: | ||
[[File:Импеданс зависит от напряжения и тока таким образом_3_09062021_0949.jpg|frame|center|Рис. 3. Импеданс зависит от напряжения и тока таким образом, как и предполагалось – по закону Ома.]] | [[File:Импеданс зависит от напряжения и тока таким образом_3_09062021_0949.jpg|frame|center|Рис. 3. Импеданс зависит от напряжения и тока таким образом, как и предполагалось – по закону Ома.|alt=Рис. 3. Импеданс зависит от напряжения и тока таким образом, как и предполагалось – по закону Ома.]] | ||
Можно сказать, что это более всеобъемлющая версия закона Ома, чем та, что рассматривалась, когда мы разбирали цепи постоянного тока (E = IR). Что неудивительно – ведь импеданс является гораздо более полным выражением сопротивления потоку тока, чем обычное сопротивление. Любое простое сопротивление и любое реактивное сопротивление, по отдельности или в комбинации (последовательно/параллельно), могут и должны быть представлены как единый импеданс в цепи переменного тока. | Можно сказать, что это более всеобъемлющая версия закона Ома, чем та, что рассматривалась, когда мы разбирали цепи постоянного тока (E = IR). Что неудивительно – ведь импеданс является гораздо более полным выражением сопротивления потоку тока, чем обычное сопротивление. Любое простое сопротивление и любое реактивное сопротивление, по отдельности или в комбинации (последовательно/параллельно), могут и должны быть представлены как единый импеданс в цепи переменного тока. | ||
| Строка 34: | Строка 34: | ||
Чтобы рассчитать ток в приведённой выше схеме, сначала необходимо указать опорный угол сдвига фаз для источника напряжения, который обычно считается равным нулю. (Фазовые углы резистивной и индуктивной составляющих импеданса всегда равны 0° и + 90° соответственно, независимо от заданных фазовых углов для напряжения или тока). | Чтобы рассчитать ток в приведённой выше схеме, сначала необходимо указать опорный угол сдвига фаз для источника напряжения, который обычно считается равным нулю. (Фазовые углы резистивной и индуктивной составляющих импеданса всегда равны 0° и + 90° соответственно, независимо от заданных фазовых углов для напряжения или тока). | ||
[[File:Рассчитываем силу тока в приведённой выше схеме_4_09062021_0949.jpg|frame|center|Рис. 4. Рассчитываем силу тока в приведённой выше схеме.]] | [[File:Рассчитываем силу тока в приведённой выше схеме_4_09062021_0949.jpg|frame|center|Рис. 4. Рассчитываем силу тока в приведённой выше схеме.|alt=Рис. 4. Рассчитываем силу тока в приведённой выше схеме.]] | ||
Как и в случае простой индуктивной цепи, волна тока отстаёт от волны напряжения (источника питания), хотя на этот раз отставание не так велико: всего 37,016° по сравнению с 90°, как в случае сугубо индуктивной цепи. | Как и в случае простой индуктивной цепи, волна тока отстаёт от волны напряжения (источника питания), хотя на этот раз отставание не так велико: всего 37,016° по сравнению с 90°, как в случае сугубо индуктивной цепи. | ||
[[File:Ток отстаёт от напряжения в последовательной LR-цепи_5_09062021_0949.jpg|frame|center|Рис. 5. Ток отстаёт от напряжения в последовательной LR-цепи на 37,016°, а не на 0° как в R-цепи и не на 90° как в L-цепи.]] | [[File:Ток отстаёт от напряжения в последовательной LR-цепи_5_09062021_0949.jpg|frame|center|Рис. 5. Ток отстаёт от напряжения в последовательной LR-цепи на 37,016°, а не на 0° как в R-цепи и не на 90° как в L-цепи.|alt=Рис. 5. Ток отстаёт от напряжения в последовательной LR-цепи на 37,016°, а не на 0° как в R-цепи и не на 90° как в L-цепи.]] | ||
Для резистора и катушки индуктивности соотношение фаз между напряжением и током не изменилось. Напряжение на резисторе синфазно (т.е. фазовый сдвиг равен 0°) с током, проходящим через этот резистор. Напряжение на катушке индуктивности на +90° не совпадает по фазе с током, проходящим через индуктор. Мы можем убедиться в этом математически: | Для резистора и катушки индуктивности соотношение фаз между напряжением и током не изменилось. Напряжение на резисторе синфазно (т.е. фазовый сдвиг равен 0°) с током, проходящим через этот резистор. Напряжение на катушке индуктивности на +90° не совпадает по фазе с током, проходящим через индуктор. Мы можем убедиться в этом математически: | ||
[[File:Фазовый угол между напряжением и током для резистора_6_09062021_0950.jpg|frame|center|Рис. 6. Фазовый угол между напряжением и током для резистора.]] | [[File:Фазовый угол между напряжением и током для резистора_6_09062021_0950.jpg|frame|center|Рис. 6. Фазовый угол между напряжением и током для резистора.|alt=Рис. 6. Фазовый угол между напряжением и током для резистора.]] | ||
Как видим, напряжение на резисторе имеет тот же фазовый угол, что и ток, проходящий через него. Это говорит нам о том, что E и I находятся в фазе (именно для резистора). А теперь посчитаем и для индуктивного элемента: | Как видим, напряжение на резисторе имеет тот же фазовый угол, что и ток, проходящий через него. Это говорит нам о том, что E и I находятся в фазе (именно для резистора). А теперь посчитаем и для индуктивного элемента: | ||
[[File:Фазовый угол между напряжением и током для катушки индуктивности_7_09062021_0950.jpg|frame|center|Рис. 7. Фазовый угол между напряжением и током для катушки индуктивности.]] | [[File:Фазовый угол между напряжением и током для катушки индуктивности_7_09062021_0950.jpg|frame|center|Рис. 7. Фазовый угол между напряжением и током для катушки индуктивности.|alt=Рис. 7. Фазовый угол между напряжением и током для катушки индуктивности.]] | ||
Напряжение на катушке индуктивности имеет фазовый угол 52,984°, в то время как ток через катушку индуктивности имеет фазовый угол -37,016° – то есть разница точно 90° между ними. Это говорит нам о том, что E и I все ещё не совпадают по фазе на 90° (это касается только катушки индуктивности). | Напряжение на катушке индуктивности имеет фазовый угол 52,984°, в то время как ток через катушку индуктивности имеет фазовый угол -37,016° – то есть разница точно 90° между ними. Это говорит нам о том, что E и I все ещё не совпадают по фазе на 90° (это касается только катушки индуктивности). | ||
| Строка 54: | Строка 54: | ||
Мы также можем математически доказать что, сложив эти комплексные значения, получим общее напряжение, в полном соответствии с правилом напряжений Кирхгофа: | Мы также можем математически доказать что, сложив эти комплексные значения, получим общее напряжение, в полном соответствии с правилом напряжений Кирхгофа: | ||
[[File:Считаем полное напряжение, используя правило Кирхгофа_8_09062021_0950.png|frame|center|Рис. 8. Считаем полное напряжение, используя правило Кирхгофа.]] | [[File:Считаем полное напряжение, используя правило Кирхгофа_8_09062021_0950.png|frame|center|Рис. 8. Считаем полное напряжение, используя правило Кирхгофа.|alt=Рис. 8. Считаем полное напряжение, используя правило Кирхгофа.]] | ||
== Расчёт с помощью программы SPICE == | == Расчёт с помощью программы SPICE == | ||
| Строка 60: | Строка 60: | ||
Проверим в программе SPICE правильность наших выкладок: | Проверим в программе SPICE правильность наших выкладок: | ||
[[File:Последовательная RL-схема_9_09062021_0950.jpg|frame|center|Рис. 9. Последовательная RL-схема.]] | [[File:Последовательная RL-схема_9_09062021_0950.jpg|frame|center|Рис. 9. Последовательная RL-схема.|alt=Рис. 9. Последовательная RL-схема.]] | ||
<syntaxhighlight lang="c" line="GESHI_NORMAL_LINE_NUMBERS|GESHI_FANCY_LINE_NUMBERS"> | <syntaxhighlight lang="c" line="GESHI_NORMAL_LINE_NUMBERS|GESHI_FANCY_LINE_NUMBERS"> | ||
| Строка 78: | Строка 78: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
[[File:SPICE выдаёт результаты не в сильно удобном для восприятия виде_10_09062021_0950.jpg|frame|center|Рис. 10. SPICE выдаёт результаты не в сильно удобном для восприятия виде, поэтому интерпретируем их.]] | [[File:SPICE выдаёт результаты не в сильно удобном для восприятия виде_10_09062021_0950.jpg|frame|center|Рис. 10. SPICE выдаёт результаты не в сильно удобном для восприятия виде, поэтому интерпретируем их.|alt=Рис. 10. SPICE выдаёт результаты не в сильно удобном для восприятия виде, поэтому интерпретируем их.]] | ||
Обратите внимание, что, как и в случае с цепью постоянного тока, SPICE выводит значения для силы тока как отрицательное число (это означает сдвиг по фазе на 180°) по сравнению с напряжением источника питания. Вместо фазового угла -37,016° мы получаем округлённый текущий фазовый угол 143° (-37° + 180°). | Обратите внимание, что, как и в случае с цепью постоянного тока, SPICE выводит значения для силы тока как отрицательное число (это означает сдвиг по фазе на 180°) по сравнению с напряжением источника питания. Вместо фазового угла -37,016° мы получаем округлённый текущий фазовый угол 143° (-37° + 180°). | ||
| Строка 88: | Строка 88: | ||
Сначала подготовим таблицу для нахождения всех значений E/I/Z, вставив те значения что известны в подходящей форме (другими словами, не нужно заносить в таблицу отдельно значения простого сопротивления и отдельно индуктивность в омах и генри соответственно; вместо этого преобразуйте их в комплексные цифры импеданса и именно их и запишите в таблицу): | Сначала подготовим таблицу для нахождения всех значений E/I/Z, вставив те значения что известны в подходящей форме (другими словами, не нужно заносить в таблицу отдельно значения простого сопротивления и отдельно индуктивность в омах и генри соответственно; вместо этого преобразуйте их в комплексные цифры импеданса и именно их и запишите в таблицу): | ||
[[File:Рассчитаем импеданс на основании пока известных данных_11_09062021_0958.jpg|frame|center|Рис. 11. Рассчитаем импеданс на основании пока известных данных и в комплексном виде занесём в таблицу.]] | [[File:Рассчитаем импеданс на основании пока известных данных_11_09062021_0958.jpg|frame|center|Рис. 11. Рассчитаем импеданс на основании пока известных данных и в комплексном виде занесём в таблицу.|alt=Рис. 11. Рассчитаем импеданс на основании пока известных данных и в комплексном виде занесём в таблицу.]] | ||
Хотя это и необязательно, я настоятельно рекомендую записать в таблицу как алгебраическую, так и полярную форму каждой величины. Если есть умеющий работать с комплексными числами калькулятор, который возьмёт на себя сложные арифметические операции без необходимости преобразования алгебраической формы в полярную, то тогда можно ограничиться только одной формой. | Хотя это и необязательно, я настоятельно рекомендую записать в таблицу как алгебраическую, так и полярную форму каждой величины. Если есть умеющий работать с комплексными числами калькулятор, который возьмёт на себя сложные арифметические операции без необходимости преобразования алгебраической формы в полярную, то тогда можно ограничиться только одной формой. | ||
| Строка 96: | Строка 96: | ||
Теперь, когда наши «заданные» цифры вставлены в соответствующие места в таблице, можно действовать так же, как и с постоянным током: определить общий импеданс из отдельных импедансов. Поскольку это последовательная цепь, мы знаем, что противодействие току (хоть простое сопротивление, хоть сложный импеданс) складывается, в результате чего получаем полное сопротивление: | Теперь, когда наши «заданные» цифры вставлены в соответствующие места в таблице, можно действовать так же, как и с постоянным током: определить общий импеданс из отдельных импедансов. Поскольку это последовательная цепь, мы знаем, что противодействие току (хоть простое сопротивление, хоть сложный импеданс) складывается, в результате чего получаем полное сопротивление: | ||
[[File:Находим общий импеданс_12_09062021_0951.jpg|frame|center|Рис. 12. Находим общий импеданс.]] | [[File:Находим общий импеданс_12_09062021_0951.jpg|frame|center|Рис. 12. Находим общий импеданс.|alt=Рис. 12. Находим общий импеданс.]] | ||
Теперь, когда известно полное напряжение и полное сопротивление, можно применить закон Ома (I = E/Z) для определения общей силы тока: | Теперь, когда известно полное напряжение и полное сопротивление, можно применить закон Ома (I = E/Z) для определения общей силы тока: | ||
[[File:Находим общую силу тока_11_09062021_0951.jpg|frame|center|Рис. 13. Находим общую силу тока.]] | [[File:Находим общую силу тока_11_09062021_0951.jpg|frame|center|Рис. 13. Находим общую силу тока.|alt=Рис. 13. Находим общую силу тока.]] | ||
Как и в случае с постоянным током, общий ток в последовательной цепи переменного тока одинаков для всех элементов. Это по-прежнему верно, потому что в последовательной цепи есть только один путь для прохождения тока, поэтому поток электронов одинаков на всём пути следования. Следовательно, мы можем просто продублировать значения силы тока как для резистора, так и для катушки индуктивности: | Как и в случае с постоянным током, общий ток в последовательной цепи переменного тока одинаков для всех элементов. Это по-прежнему верно, потому что в последовательной цепи есть только один путь для прохождения тока, поэтому поток электронов одинаков на всём пути следования. Следовательно, мы можем просто продублировать значения силы тока как для резистора, так и для катушки индуктивности: | ||
[[File:В последовательной цепи сила тока для отдельных элементов такая же_14_09062021_0951.jpg|frame|center|Рис. 14. В последовательной цепи сила тока для отдельных элементов такая же, как и общая сила тока.]] | [[File:В последовательной цепи сила тока для отдельных элементов такая же_14_09062021_0951.jpg|frame|center|Рис. 14. В последовательной цепи сила тока для отдельных элементов такая же, как и общая сила тока.|alt=Рис. 14. В последовательной цепи сила тока для отдельных элементов такая же, как и общая сила тока.]] | ||
Теперь все, что осталось вычислить, – это падение напряжения на резисторе и катушке индуктивности соответственно. Это делается с помощью закона Ома (E = IZ), применяемого вертикально в каждом столбце таблицы: | Теперь все, что осталось вычислить, – это падение напряжения на резисторе и катушке индуктивности соответственно. Это делается с помощью закона Ома (E = IZ), применяемого вертикально в каждом столбце таблицы: | ||
[[File:Последний шаг – нахождение по закону Ома напряжения для отдельных элементов_15_09062021_0952.jpg|frame|center|Рис. 15. Последний шаг – нахождение по закону Ома напряжения для отдельных элементов.]] | [[File:Последний шаг – нахождение по закону Ома напряжения для отдельных элементов_15_09062021_0952.jpg|frame|center|Рис. 15. Последний шаг – нахождение по закону Ома напряжения для отдельных элементов.|alt=Рис. 15. Последний шаг – нахождение по закону Ома напряжения для отдельных элементов.]] | ||
На этом заполнение нашей таблицы завершено. Точно такие же правила, которые мы применяли при анализе цепей постоянного тока, применимы и к цепям переменного тока. Но с оговоркой: все величины должны быть представлены и вычислены в комплексной, а не в скалярной форме. | На этом заполнение нашей таблицы завершено. Точно такие же правила, которые мы применяли при анализе цепей постоянного тока, применимы и к цепям переменного тока. Но с оговоркой: все величины должны быть представлены и вычислены в комплексной, а не в скалярной форме. | ||
| Строка 126: | Строка 126: | ||
Импеданс (Z) последовательной RL-цепи может быть вычислен с учётом сопротивления (R) и индуктивного реактивного сопротивления (XL). Поскольку E = IR, E = IXL и E = IZ, то обычное сопротивление, реактивное сопротивление и импеданс пропорциональны соответствующему напряжению. Таким образом, векторную диаграмму для напряжения можно заменить на аналогичную диаграмму для импеданса. | Импеданс (Z) последовательной RL-цепи может быть вычислен с учётом сопротивления (R) и индуктивного реактивного сопротивления (XL). Поскольку E = IR, E = IXL и E = IZ, то обычное сопротивление, реактивное сопротивление и импеданс пропорциональны соответствующему напряжению. Таким образом, векторную диаграмму для напряжения можно заменить на аналогичную диаграмму для импеданса. | ||
[[File:В последовательной RL-цепи вектор для импеданса такой же_16_09062021_0952.jpg|frame|center|Рис. 16. В последовательной RL-цепи вектор для импеданса такой же, как и вектор для напряжения.]] | [[File:В последовательной RL-цепи вектор для импеданса такой же_16_09062021_0952.jpg|frame|center|Рис. 16. В последовательной RL-цепи вектор для импеданса такой же, как и вектор для напряжения.|alt=Рис. 16. В последовательной RL-цепи вектор для импеданса такой же, как и вектор для напряжения.]] | ||
'''Пример:''' Дано: резистор на 40 Ом, соединён последовательно с катушкой индуктивности на 79,58 миллигенри. Найти: полное сопротивление при частоте 60 Гц. | '''Пример:''' Дано: резистор на 40 Ом, соединён последовательно с катушкой индуктивности на 79,58 миллигенри. Найти: полное сопротивление при частоте 60 Гц. | ||
Версия от 19:09, 17 ноября 2021
Последовательные резистивно-индуктивные цепи[1]
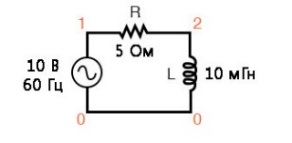
В предыдущем разделе мы исследовали простые цепи переменного тока, помимо источника напряжения содержащих или только резистор или только катушку индуктивности. Теперь мы последовательно соединим и то и другое и посмотрим, что получится.
Пример последовательной схемы «резистор-индуктор»
Возьмем такую схему в качестве первого примера:
В индуктивной цепи, в которой помимо катушки есть последовательный резистор, волна тока будет отставать от волны приложенного напряжения в пределах от 0° до 90°.
Резистор оказывает 5 Ом обычного сопротивления и это значение не зависит от частоты тока. В то же время катушка индуктивности оказывает 3.7699 Ом реактивного сопротивления переменному тока с частотой 60 Гц. Поскольку сопротивление резистора является действительным числом («5 Ом ∠ 0°», или, если в комплексных числах, «5 + j0 Ом»), а реактивное сопротивление катушки индуктивности - мнимым числом («3,7699 Ом ∠ 90°» или «0 + j3,7699 Ом»). Совокупный эффект двух этих элементов цепи противодействует переменному току и данное суммарное сопротивление равно сумме двух комплексных чисел.
Это комбинированное противодействие является векторной комбинацией обычного сопротивления и реактивного сопротивления. Чтобы выразить это более лаконично, понадобится более общий термин для обозначения сопротивления току, нежели простое сопротивление или реактивное сопротивление.
Этот термин называется импедансом, обозначается буквой «Z». Выражается в единицах «Ом», точно так же, как простое сопротивление и реактивное сопротивление. В приведённом выше примере полное сопротивление цепи составляет:

Сопротивление в соответствии с законом Ома
Импеданс ожидаемо связан по закону Ома с напряжением и током аналогично обычному сопротивлению:

Можно сказать, что это более всеобъемлющая версия закона Ома, чем та, что рассматривалась, когда мы разбирали цепи постоянного тока (E = IR). Что неудивительно – ведь импеданс является гораздо более полным выражением сопротивления потоку тока, чем обычное сопротивление. Любое простое сопротивление и любое реактивное сопротивление, по отдельности или в комбинации (последовательно/параллельно), могут и должны быть представлены как единый импеданс в цепи переменного тока.
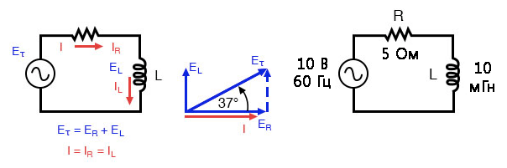
Чтобы рассчитать ток в приведённой выше схеме, сначала необходимо указать опорный угол сдвига фаз для источника напряжения, который обычно считается равным нулю. (Фазовые углы резистивной и индуктивной составляющих импеданса всегда равны 0° и + 90° соответственно, независимо от заданных фазовых углов для напряжения или тока).
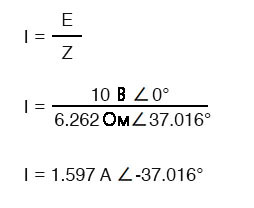
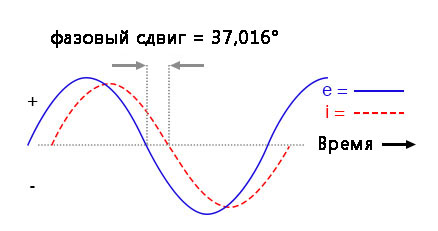
Как и в случае простой индуктивной цепи, волна тока отстаёт от волны напряжения (источника питания), хотя на этот раз отставание не так велико: всего 37,016° по сравнению с 90°, как в случае сугубо индуктивной цепи.
Для резистора и катушки индуктивности соотношение фаз между напряжением и током не изменилось. Напряжение на резисторе синфазно (т.е. фазовый сдвиг равен 0°) с током, проходящим через этот резистор. Напряжение на катушке индуктивности на +90° не совпадает по фазе с током, проходящим через индуктор. Мы можем убедиться в этом математически:

Как видим, напряжение на резисторе имеет тот же фазовый угол, что и ток, проходящий через него. Это говорит нам о том, что E и I находятся в фазе (именно для резистора). А теперь посчитаем и для индуктивного элемента:

Напряжение на катушке индуктивности имеет фазовый угол 52,984°, в то время как ток через катушку индуктивности имеет фазовый угол -37,016° – то есть разница точно 90° между ними. Это говорит нам о том, что E и I все ещё не совпадают по фазе на 90° (это касается только катушки индуктивности).
Использование правила напряжений Кирхгофа
Мы также можем математически доказать что, сложив эти комплексные значения, получим общее напряжение, в полном соответствии с правилом напряжений Кирхгофа:
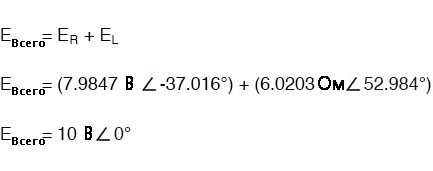
Расчёт с помощью программы SPICE
Проверим в программе SPICE правильность наших выкладок:
v1 1 0 ac 10 sin
r1 1 2 5
l1 2 0 10m
.ac lin 1 60 60
.print ac v(1,2) v(2,0) i(v1)
.print ac vp(1,2) vp(2,0) ip(v1)
.end
freq v(1,2) v(2) i(v1)
6.000E+01 7.985E+00 6.020E+00 1.597E+00
freq vp(1,2) vp(2) ip(v1)
6.000E+01 -3.702E+01 5.298E+01 1.430E+0

Обратите внимание, что, как и в случае с цепью постоянного тока, SPICE выводит значения для силы тока как отрицательное число (это означает сдвиг по фазе на 180°) по сравнению с напряжением источника питания. Вместо фазового угла -37,016° мы получаем округлённый текущий фазовый угол 143° (-37° + 180°).
Это всего лишь проявление идиосинкразии (показания в противоположной направленности) программы SPICE и ничего более. Обратите внимание, что фазы напряжения резистора и катушки индуктивности совпадают с нашими расчётами (-37,02° и 52,98° соответственно), тут всё как мы и ожидали.
Имея эти начальные данные, мы можем рассчитать остальные электрические характеристики всех элементов цепи. Но, пожалуй, даже для такой простой последовательной схемы целесообразно использовать «табличный метод». Применение этого метода к этой простой последовательной схеме «резистор-индуктор» принципиально не отличается от того, как мы это делали раньше для схем постоянного тока.
Сначала подготовим таблицу для нахождения всех значений E/I/Z, вставив те значения что известны в подходящей форме (другими словами, не нужно заносить в таблицу отдельно значения простого сопротивления и отдельно индуктивность в омах и генри соответственно; вместо этого преобразуйте их в комплексные цифры импеданса и именно их и запишите в таблицу):
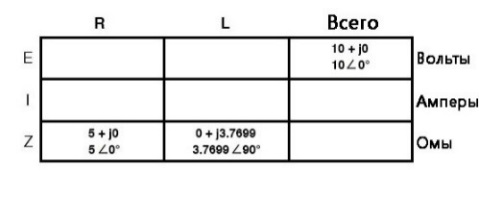
Хотя это и необязательно, я настоятельно рекомендую записать в таблицу как алгебраическую, так и полярную форму каждой величины. Если есть умеющий работать с комплексными числами калькулятор, который возьмёт на себя сложные арифметические операции без необходимости преобразования алгебраической формы в полярную, то тогда можно ограничиться только одной формой.
Однако, если приходится выполнять сложные арифметические операции вручную (сложение и вычитание проще делать в алгебраической форме, а умножение и деление – в полярной), запись каждой величины в обеих формах действительно пригодится.
Теперь, когда наши «заданные» цифры вставлены в соответствующие места в таблице, можно действовать так же, как и с постоянным током: определить общий импеданс из отдельных импедансов. Поскольку это последовательная цепь, мы знаем, что противодействие току (хоть простое сопротивление, хоть сложный импеданс) складывается, в результате чего получаем полное сопротивление:

Теперь, когда известно полное напряжение и полное сопротивление, можно применить закон Ома (I = E/Z) для определения общей силы тока:

Как и в случае с постоянным током, общий ток в последовательной цепи переменного тока одинаков для всех элементов. Это по-прежнему верно, потому что в последовательной цепи есть только один путь для прохождения тока, поэтому поток электронов одинаков на всём пути следования. Следовательно, мы можем просто продублировать значения силы тока как для резистора, так и для катушки индуктивности:

Теперь все, что осталось вычислить, – это падение напряжения на резисторе и катушке индуктивности соответственно. Это делается с помощью закона Ома (E = IZ), применяемого вертикально в каждом столбце таблицы:
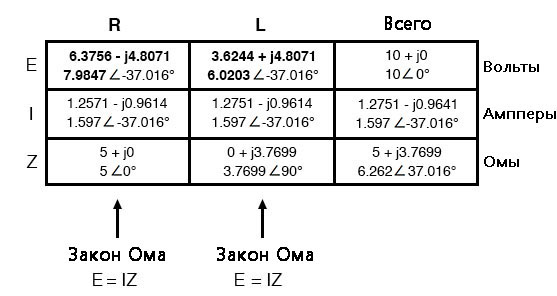
На этом заполнение нашей таблицы завершено. Точно такие же правила, которые мы применяли при анализе цепей постоянного тока, применимы и к цепям переменного тока. Но с оговоркой: все величины должны быть представлены и вычислены в комплексной, а не в скалярной форме.
Если фазовый сдвиг в наших расчётах указан правильно, нет принципиальной разницы в том, как мы подходим к основному анализу цепи переменного тока по сравнению с анализом цепи постоянного тока.
Сейчас самое время, чтобы сопоставить эти расчётные цифры и те показания, которые будут получены с помощью приборов при реальных измерениях напряжения и силы тока.
Цифры, которые напрямую относятся к реальным измерениям, будут в полярной форме, а не в алгебраической! Другими словами, если вы подключите вольтметр к резистору в этой цепи, он будет показывать 7,9847 вольт (полярная форма записи), а не 6,3756 (вещественная составляющая алгебраической формы записи) или 4,8071 (мнимая составляющая алгебраической формы записи) вольт.
В контексте графика, измерительные приборы просто сообщат длину вектора для конкретной величины (напряжения или тока).
Алгебраическая запись удобна для арифметического сложения и вычитания, но при этом она более абстрактная. Полярная запись к реальным измерениям ближе. Как уже говорилось, в таблицах, ради упрощения математических расчётах, мы будем указывать как полярную, так и алгебраическую запись для каждой величины.
Это не является абсолютно необходимым, но однозначно полезно для тех, кто не использует калькулятор с расширенными возможностями. Если использовать только одну формы записи, то лучше тогда полярную, потому что она напрямую коррелирована с реальными измерениями.
Импеданс (Z) последовательной RL-цепи может быть вычислен с учётом сопротивления (R) и индуктивного реактивного сопротивления (XL). Поскольку E = IR, E = IXL и E = IZ, то обычное сопротивление, реактивное сопротивление и импеданс пропорциональны соответствующему напряжению. Таким образом, векторную диаграмму для напряжения можно заменить на аналогичную диаграмму для импеданса.
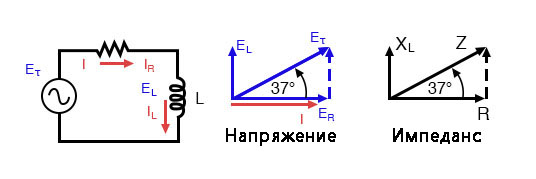
Пример: Дано: резистор на 40 Ом, соединён последовательно с катушкой индуктивности на 79,58 миллигенри. Найти: полное сопротивление при частоте 60 Гц.
XL = 2πfL
XL = 2π × 60 × 79,58 × 10-3
XL = 30 Ом
Z = R + jXL
Z = 40 + j30
|Z| = sqrt(402 + 302) = 50 Ом
∠Z = arctng(30/40) = 36.87°
Z = 40 + j30 = 50 ∠36.87°
Итог
- Импеданс – это полная мера противодействия электрическому току и представляет собой комплексную (векторную) сумму простого сопротивления («вещественная составляющая») и реактивного сопротивления («мнимая составляющая»). Импеданс обозначается буквой «Z» и измеряется в Омах, так же как и сопротивление (R) и реактивное сопротивление (X).
- К импедансу (Z) применимы те же приёмы, которые используются при работе с сопротивлением (R) при анализе последовательной цепи. Последовательное сопротивление складывается, чтобы вычислить общий импеданс. При этом все вычисления обязательно нужно выполнять в комплексной (не скалярной) форме! ZВсего = Z1 + Z2 + … + Zn.
- Сугубо резистивный импеданс имеет фазовый угол, равный точно 0 ° (ZR = R Ом ∠ 0°).
- Сугубо индуктивный импеданс имеет фазовый угол, равный точно +90° (ZL = XL Ом ∠ 90 °).
- Закон Ома для цепей переменного тока: E = IZ; I = E/Z; Z = E/I.
- Когда в последовательной цепи есть и резисторы, и катушки индуктивности, общий импеданс будет иметь фазовый угол где-то между 0° и +90°. Ток в цепи будет иметь фазовый угол в пределах от 0° до -90°.
- Последовательные цепи переменного тока обладают теми же фундаментальными свойствами, что и последовательные цепи постоянного тока: ток однороден по всей цепи, чтобы найти общее напряжение – падения напряжения отдельных элементов складываются, а импедансы компонентов суммируются, чтобы получить общий импеданс.
См.также
Внешние ссылки