Электроника:Цифровая электроника/Двоичная арифметика/Двоичное сложение: различия между версиями
Valemak (обсуждение | вклад) Нет описания правки |
Myagkij (обсуждение | вклад) (добавление внутренних ссылок на страницу, добавление в категории) |
||
| Строка 24: | Строка 24: | ||
== Бинарное сложение – основа цифровых компьютеров == | == Бинарное сложение – основа цифровых компьютеров == | ||
Как мы увидим позже, существуют способы создания электронных схем для выполнения этой самой задачи сложения, представляя каждый бит каждого двоичного числа как сигнал напряжения (либо «высокий» для единицы, либо «низкий» для нуля). Это самая основа всей арифметики, на которой работают современные цифровые | Как мы увидим позже, существуют способы создания электронных схем для выполнения этой самой задачи сложения, представляя каждый бит каждого двоичного числа как сигнал напряжения (либо «высокий» для единицы, либо «низкий» для нуля). Это самая основа всей арифметики, на которой работают современные цифровые [[компьютер]]ы. | ||
=См.также= | =См.также= | ||
| Строка 36: | Строка 36: | ||
{{Навигационная таблица/Электроника}} | {{Навигационная таблица/Электроника}} | ||
{{Навигационная таблица/Телепорт}} | {{Навигационная таблица/Телепорт}} | ||
[[Категория:Цифровая электроника]] | |||
[[Категория:Двоичная арифметика]] | |||
[[Категория:Двоичное сложение]] | |||
Версия от 09:41, 5 ноября 2021
Двоичное сложение[1]
Принципы двоичного сложения
Сложение двоичных чисел – очень простая задача, очень похожая на ручное сложение десятеричных чисел. Как и в случае с десятеричными числами, можно начать с размещения битов (цифр) по столбцам, т.е. позиционируем цифры с учётом веса разряда справа-налево. В общем, старое доброе складывание чисел столбиком.
В отличие от десятеричного сложения, правила сложения двоичных разрядов нужно запоминать в меньшем количестве:
| 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 1 + 1 + 1 = 11 |
Как и в случае с десятеричным сложением, когда сумма в одном столбце представляет собой двухразрядное (двузначное) число, менее значимая цифра записывается как часть общей суммы в этом столбце, а более значимая цифра «переносится» в следующий столбец левее. Рассмотрим на примерах:
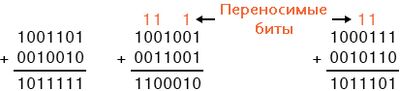
Самое левое сложение не потребовало переноса каких-либо битов, поскольку сумма битов в каждом столбце была либо 1, либо 0, а не 102 или 112. В двух других примерах определённо присутствуют переносимые биты, но процесс сложения всё ещё довольно-таки прост.
Бинарное сложение – основа цифровых компьютеров
Как мы увидим позже, существуют способы создания электронных схем для выполнения этой самой задачи сложения, представляя каждый бит каждого двоичного числа как сигнал напряжения (либо «высокий» для единицы, либо «низкий» для нуля). Это самая основа всей арифметики, на которой работают современные цифровые компьютеры.
См.также
Внешние ссылки