| Теория по электронике |
|---|
| Постоянный ток |
|---|
| Основные концепты электричества |
• Статическое электричество • Проводники, диэлектрики и поток электронов • Что такое электрические цепи • Напряжение и электроток • Сопротивление • Напряжение и электроток в реальной цепи • Условный ток и поток электронов |
|---|
| Закон Ома |
• Закон Ома – Как напряжение, сила тока и сопротивление связаны друг с другом • Аналогия для закона Ома • Мощность в электрических цепях • Расчёт электрической мощности • Резисторы • Нелинейная проводимость • Построение цепи • Полярность перепада напряжения • Компьютерная симуляция электрических цепей |
|---|
| Правила электробезопасности |
• Важность правил электробезопасности • Воздействие электричества на психологическое состояние • Путь, который ток проходит перед ударом • Закон Ома (снова!) • Техника безопасности • Первая медицинская помощь при ударе током • Распространённые источники опасности • Проектирование электроцепей с учётом требований безопасности • Безопасное использование приборов для измерения электрических показателей • Данные о влиянии удара током на тело человека |
|---|
| Экспоненциальная запись и метрические приставки |
• Экспоненциальная запись • Арифметические операции для экспоненциальной записи • Метрические обозначения • Преобразование метрических приставок • Используем ручной калькулятор • Экспоненциальная форма в программе SPICE |
|---|
| Последовательные и параллельные электрические цепи |
• Что такое «последовательные» и «параллельные» электрические цепи • Простая последовательная цепь • Простая параллельная цепь • Электропроводность • Рассчитываем мощность • Правильно используем закон Ома • Анализ отказов компонентов цепи • Строим простые резистивные цепи |
|---|
| Схемы с делителями напряжения и правила Кирхгофа |
• Схемы с делителем напряжения • Правило напряжений Кирхгофа (ПНК) • Цепи – делители тока и формула делителя тока • Правило Кирхгофа для силы тока (ПКТ) |
|---|
| Комбинированные последовательно-параллельные схемы |
• Что такое последовательно-параллельная цепь • Методы анализа последовательно-параллельных резисторных цепей • Перерисовываем избыточно усложнённые схемы • Анализ отказов компонентов (продолжение) • Построение простых резисторных цепей |
|---|
| Измерения в электрических цепях постоянного тока |
• Что такое измеритель? • Как устроен вольтметр • Как вольтметр влияет на измеряемую цепь • Как устроен амперметр • Как амперметр влияет на измеряемую цепь • Как устроен омметр • Высоковольтный омметр • Мультиметры • Кельвиновское 4-проводное измерение сопротивления • Мостовые схемы • Как устроен ваттметр • Как самостоятельно сделать ручной калибратор |
|---|
| Сигналы электрического оборудования |
• Аналоговые и цифровые сигналы • Системы сигналов напряжения • Системы сигналов силы тока • Тахогенераторы • Теромопары • Измерения pH • Тензодатчики |
|---|
| Анализ сети постоянного тока |
• Что такое сетевой анализ? • Метод токов ветвей • Аналитический метод контурных токов • Метод узловых потенциалов • Введение в сетевые теоремы • Теорема Миллмана • Теорема о суперпозиции • Теорема Тевенена • Теорема Нортона • Эквивалентность схем Тевенена и Нортона • И вновь о теореме Миллмана • Теорема о передаче максимальной мощности • Δ-Y и Y-Δ преобразования |
|---|
| Батареи и системы питания |
• Поведение электронов при химических реакциях • Батарейные конструкции • Рейтинг батарей • Батареи специального назначения • Практические рекомендации при использовании батарей |
|---|
| Физика проводников и диэлектриков |
• Введение в физику проводников и диэлектриков • Размеры проводов• Допустимые токовые нагрузки на провода • Предохранители • Удельное сопротивление • Температурный коэффициент сопротивления • Сверхпроводимость • Пробивное напряжение диэлектрика |
|---|
| Конденсаторы |
• Электрическое поле и ёмкость • Конденсаторы и дифференциальное исчисление • Факторы, влияющие на ёмкость конденсатора • Последовательное и параллельное соединение конденсаторов • Практические соображения - Конденсаторы |
|---|
| Магнетизм и электромагнетизм |
• Постоянные магниты • Электромангетизм • Единицы измерения магнитных величин • Магнитная проницаемость и насыщение • Электромагнитная индукция • Взаимная индукция |
|---|
| Катушки индуктивности |
• Магнитные поля и индуктивность • Катушки индуктивности и дифференциальное исчисление • Факторы, влияющие на индуктивность • Катушки индуктивности в последовательных и параллельных соединениях • Практические соображения – Катушки индуктивности |
|---|
| Постоянные времени в RC и L/R цепях |
• Переходные процессы в электрических цепях • Переходные процессы в цепях с конденсатором • Переходные процессы в цепях с катушкой индуктивности • Расчёт напряжения и силы тока • Почему L/R, а не LR? • Комплексные расчёты напряжения и тока • Сложные схемы • Расчёт неизвестного времени |
|---|
| Переменный ток |
|---|
| Основы теории переменного тока |
• Что такое переменный ток? • Формы волн переменного тока • Измерение величин переменного тока • Расчёт простейшей цепи переменного тока • Фаза переменного тока • Принципы радио |
|---|
| Комплексные числа |
• Введение в комплексные числа • Векторы и волны переменного тока • Сложение простых векторов • Сложение сложных векторов • Полярная и алгебраическая запись комплексных чисел • Арифметика комплексных чисел • И ещё по поводу полярности переменного тока • Несколько примеров с цепями переменного тока |
|---|
| Реактанс и импеданс – Индуктивность |
• Резистор в цепи переменного тока (Индуктивность) • Катушка индуктивности в цепи переменного тока • Последовательные резистивно-индуктивные цепи • Параллельные резистивно-индуктивные цепи • Особенности катушек индуктивности • Что такое «скин-эффект»? |
|---|
| Реактанс и импеданс – Ёмкость |
• Резистор в цепи переменного тока (Ёмкость) • Конденсатор в цепи переменного тока • Последовательные резистивно-ёмкостные цепи • Параллельные резистивно-ёмкостные цепи • Особенности конденсаторов |
|---|
| Реактанс и импеданс – R/L/C-цепи |
• Обзор R, X и Z (сопротивление, реактанс и импеданс) • Последовательные R/L/C-цепи • Параллельные R/L/C-цепи • Последовательно-параллельные R/L/C-цепи • Реактивная проводимость и адмиттанс • R/L/C-цепи – что в итоге? |
|---|
| Резонанс |
• Электрический маятник • Простой параллельный резонанс (колебательный контур) • Простой последовательный резонанс • Применение резонанса • Резонанс в последовательно-параллельных цепях • Добротность и полоса пропускания резонансной цепи |
|---|
| Сигналы переменного тока смешанной частоты |
• Сигналы переменного тока смешанной частоты - Введение • Прямоугольные волновые сигналы • Другие волновые формы • Подробнее о спектральном анализе • Эффекты в электрических цепях |
|---|
| Фильтры |
• Что такое фильтр? • Низкочастотные фильтры • Высокочастотные фильтры • Полосовые фильтры • Полосно-заграждающие фильтры • Резонансные фильтры • Подводя итоги по фильтрам |
|---|
| Трансформаторы |
• Взаимная индуктивность и основные операции • Повышающие и понижающие трансформаторы • Электрическая изоляция • Фазировка • Конфигурации обмотки • Регулировка напряжения • Специальные трансформаторы и приложения • Практические соображения – Трансформаторы |
|---|
| Многофазные цепи переменного тока |
• Однофазные системы питания • Трёхфазные системы питания • Чередование фаз • Устройство многофазного двигателя • Трёхфазные Y- и дельта-конфигурации • Трёхфазные цепи с трансформатором • Гармоники в многофазных энергосистемах • Гармонические фазовые последовательности |
|---|
| Коэффициент мощности |
• Мощность в резистивных и реактивных цепях переменного тока • Истинная, реактивная и полная мощность • Расчёт коэффициента мощности • Практическая коррекция коэффициента мощности |
|---|
| Измерение цепей переменного тока |
• Вольтметры и амперметры переменного тока • Измерение частоты и фазы • Измерение мощности • Измерение качества электроэнергии • Мостовые схемы переменного тока • Измерительные преобразователи переменного тока |
|---|
| Двигатели переменного тока |
• Введение в двигатели переменного тока • Синхронные двигатели • Синхронный конденсатор • Двигатель с магнитным сопротивлением • Шаговые двигатели • Бесщёточный двигатель постоянного тока • Многофазные асинхронные двигатели Теслы • Асинхронные двигатели с фазным ротором • Однофазные асинхронные двигатели • Прочие специализированные двигатели • Сельсин-двигатели (синхронизированные двигатели) • Коллекторные двигатели переменного тока |
|---|
| Линии передачи |
• Кабель на 50 Ом? • Электрические цепи и скорость света • Характеристический импеданс • Линии передачи конечной длины • «Длинные» и «короткие» линии передачи • Стоячие волны и резонанс • Преобразование импеданса • Волноводы |
|---|
| Полупроводники |
|---|
| Усилители и активные устройства |
• От электрики к электронике • Активные и пассивные устройства • Усилители • Коэффициент усиления • Децибелы • Абсолютные дБ-шкалы • Аттенюаторы |
|---|
| Теория твердотельных приборов |
• Введение в теорию твердотельных устройств • Квантовая физика • Валентность и кристаллическая структура • Зонная теория твёрдых тел • Электроны и «дырки» • P-N-переход • Полупроводниковые диоды • Транзисторы с биполярным переходом • Полевые транзисторы • Полевые транзисторы с изолированным затвором (MOSFET) • Тиристоры • Методы производства полупроводников • Сверхпроводящие устройства • Квантовые устройства • Полупроводниковые приборы в SPICE |
|---|
| Диоды и выпрямители |
• Диоды и выпрямители – Введение • Проверка диодов мультиметром • Номинальные характеристики диодов • Схемы выпрямителей • Пиковый детектор • Схемы ограничителей напряжения • Схемы фиксаторов уровня • Умножители напряжения (удвоители, утроители, учетверители и т.д.) • Схемы коммутации индуктивных нагрузок • Диодные схемы коммутации • Что такое диод Зенера (стабилитрон)? • Диоды специального назначения • Прочие диодные технологии • Модели диодов в SPICE |
|---|
| Биполярные транзисторы |
• Транзисторы с биполярным переходом (ТБП) – Введение • Транзистор с биполярным переходом (ТБП) как переключатель • Проверка транзистора с биполярным переходом (ТБП) с помощью мультиметра • Активный режим работы транзистора с биполярным переходом (ТБП) • Усилительный каскад с общим эмиттером • Усилительный каскад с общим коллектором • Усилительный каскад с общей базой • Каскодный усилитель • Методы смещения для транзисторов с биполярным переходом (ТБП) • Расчёт смещения для транзисторов с биполярным переходом (ТБП) • Взаимодействие входа и выхода в транзисторах с биполярным переходом (ТБП) • Обратная связь в транзисторах с биполярным переходом (ТБП) • Импеданс усилителя • Токовые зеркала в транзисторах с биполярным переходом (ТБП) • Параметры и корпуса транзисторов с биполярным переходом (ТБП) • Особенности транзисторов с биполярным переходом (ТБП) |
|---|
| Полевые транзисторы |
• Полевые транзисторы (JFET) – Введение • Полевой транзистор (JFET) как переключатель • Проверка полевого транзистора (JFET) с помощью мультиметра • Активный режим работы полевого транзистора (JFET) |
|---|
| Полевые транзисторы с изолированным затвором |
• Полевые транзисторы с изолированным затвором – Введение • Обедняющие полевые транзисторы с изолированным затвором • Биполярные транзисторы с изолированным затвором |
|---|
| Тиристоры |
• Гистерезис • Газоразрядные лампы • Диод Шокли (динистор) • DIAC (симметричный динистор) • Управляемый кремниевый выпрямитель (SCR-тиристор) • TRIAC (симметричный тринистор, триак) • Оптотиристоры • Однопереходной транзистор • Управляемый кремниевый коммутатор (SCS-тиристор) • Тиристоры с полевым управлением |
|---|
| Операционные усилители |
• Операционные усилители (ОУ) – Введение • Несимметричные и дифференциальные усилители • «Операционный» усилитель • Отрицательная обратная связь • Делитель напряжения в цепи обратной связи • Аналогия для делителя напряжения в цепи обратной связи • Преобразование сигнала напряжения в сигнал тока • Схемы усреднителя и сумматора • Построение дифференциальных усилителей • Инструментальный (измерительный) усилитель • Схемы дифференциатора и интегратора • Положительная обратная связь • Практические аспекты ОУ • Модели операционных усилителей |
|---|
| Практические аналоговые полупроводниковые схемы |
• Электростатический разряд • Схемы источников питания • Схемы усилителей • Осцилляторные схемы • Радиосхемы • Вычислительные схемы • Измерительные схемы |
|---|
| Приводы двигателей постоянного тока |
• Широтно-импульсная модуляция |
|---|
| Электронные лампы |
• Электронные лампы – Введение • История электронных ламп – с чего всё началось • Триод • Тетрод • Силовой лучевой тетрод • Пентод • Комбинированные электронные лампы • Характеристики электронных ламп • Ионизированные (газовые) электронные лампы • Индикаторные электронные лампы • Микроволновые электронные лампы • Сравниваем электронные лампы и полупроводники |
|---|
| Цифровая электроника |
|---|
| Системы счисления |
• Числа и способы их выражения • Системы счисления • Сравниваем десятеричные и двоичные числа • Восьмеричная и шестнадцатеричная системы счисления • Восьмеричные и шестнадцатеричные числа преобразовываем в десятеричные • Преобразование из десятеричной системы счисления |
|---|
| Двоичная арифметика |
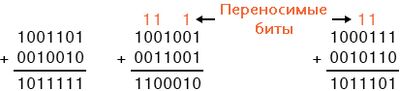
• Числа и системы счисления • Двоичное сложение • Отрицательные двоичные числа • Двоичное вычитание • Двоичное переполнение • Наборы битов |
|---|
| Логические вентили |
• Цифровые сигналы и вентили • Вентили «НЕ» • «Буферные» вентили • Вентили с более чем одним входом • Транзисторно-транзисторная логика вентилей «И-НЕ» и «И» • Транзисторно-транзисторная логика вентилей «ИЛИ-НЕ» и «ИЛИ» • Схемы КМОП-вентилей • Специальные выходы в вентилях • Универсальность вентилей «И-НЕ» и «ИЛИ-НЕ» • Уровни напряжения для «высоких» и «низких» логических сигналов • Вентильные DIP корпусы |
|---|
| Переключатели |
• Типы переключателей • Как устроены контакты переключателей • «Нормальное» состояние контакта и последовательное замыкание/размыкание • «Дребезжание» контактов |
|---|
| Электромеханические реле |
• Устройство реле • Контакторы • Реле с задержкой времени • Защитные реле • Твердотельные реле |
|---|
| Релейная логика |
• «Лестничные» диаграммы • Функции цифровой логики • Разрешающие и блокирующие схемы • Схемы управления двигателем • Отказоустойчивость • Программируемые логические контроллеры (ПЛК) |
|---|
| Булева алгебра |
• Булева алгебра – Введение • Логическая арифметика • Булевы алгебраические тождества • Булевы алгебраические свойства • Логические правила для упрощения • Примеры упрощения схем • Функция «Исключающее ИЛИ»: вентиль XOR • Законы де Моргана • Преобразование таблиц истинности в логические выражения |
|---|
| Карты Карно |
• Карты Карно – Введение • Диаграммы Венна и множества • Булевы соотношения на диаграммах Венна • Преобразование диаграмм Венна в карты Карно • Карты Карно, таблицы истинности и логические выражения • Упрощение логики с помощью карт Карно • Бо́льшие карты Карно с 4-мя переменными • Минтермы и макстермы в реализациях • Обозначения сумм и произведений • Поля «безразличия» на картах Карно • Бо́льшие карты Карно с 5-ю и 6-ю переменными |
|---|
| Функции комбинационной логики |
• Функции комбинационной логики – Введение • Неполный сумматор • Полный сумматор • Декодер • Кодер • Демультиплексоры • Мультиплексоры • Совместное использование множественных комбинационных схем |
|---|
| Мультивибраторы |
• Цифровая логика с обратной связью • SR-защёлка • Вентильная SR-защёлка • D-защёлка • Защёлки с запуском по фронту сигнала: триггеры • JK-триггер • Триггеры с асинхронными входами • Моностабильные мультивибраторы |
|---|
| Схемы последовательностей |
• Двоичная счётная последовательность • Асинхронные счётчики • Синхронные счётчики • Конечные автоматы |
|---|
| Сдвиговые регистры |
• Сдвиговые регистры – Введение • Сдвиговые регистры: последовательный вход, последовательный выход (SISO) • Сдвиговые регистры: параллельный вход, последовательный выход (PISO) • Сдвиговые регистры: последовательный вход, параллельный выход (SIPO) • Универсальные сдвиговые регистры: параллельный вход, параллельный выход (PIPO) • Кольцевые счётчики |
|---|
| Цифро-аналоговые и аналого-цифровые преобразования |
• Цифро-аналоговые (ЦАП) и аналого-цифровые (АЦП) преобразования – Введение • ЦАП R/2nR: цифро-аналоговый преобразователь с двоично-взвешенным входом • ЦАП R/2R: (цифро-аналоговый преобразователь) • Параллельные АЦП • Цифровые ступенчатые АЦП • АЦП с последовательным приближением • Отслеживающий АЦП • Скатные (интегрирующие) АЦП • Дельта-сигма АЦП • Практические аспекты схем АЦП |
|---|
| Цифровая связь |
• Цифровая связь – Введение • Сети и шины • Потоки данных • Типы электрических сигналов • Оптическая передача данных • Топология сети • Сетевые протоколы • Практические аспекты цифровой связи |
|---|
| Цифровое хранилище (память) |
• Почему «цифровое»? • Понятия и концепции цифровой памяти • Современная немеханическая память • Устаревшие немеханические технологии памяти • Постоянное запоминающее устройство (ПЗУ) • Память с движущимися частями: «Приводы» |
|---|
| Принципы цифровых вычислений |
• Двоичный сумматор • Таблицы поиска • Конечные автоматы • Микропроцессоры • Микропроцессорное программирование |
|---|
| Справочные материалы |
|---|
| Полезные уравнения и коэффициенты пересчёта |
• Уравнения и законы для цепей постоянного тока • Правила последовательных цепей • Правила параллельных цепей • Эквивалентные значения компонентов в последовательных и параллельных цепях • Уравнение ёмкости конденсатора • Уравнение катушки индуктивности • Уравнения постоянной времени • Уравнения цепей переменного тока • Уравнения для децибел • Метрические приставки и преобразования единиц измерения |
|---|
| Цветовая маркировка |
• Цветовая маркировка резисторов • Цветовая маркировка проводки • Инфографика цветовой маркировки проводки |
|---|
| Таблицы проводников и диэлектриков |
• Таблица калибров медной проволоки • Таблица допустимых нагрузок для медного провода • Коэффициенты удельного сопротивления • Таблица температурных коэффициентов сопротивления • Критические температуры для сверхпроводников • Диэлектрическая прочность изоляторов |
|---|
| Справочник по алгебре |
• Основные алгебраические тождества • Основные свойства арифметики • Свойства степеней • Извлечение корней • Важные константы • Логарифмы • Формулы сокращённого умножения • Квадратное уравнение • Прогрессии • Факториалы • Решение систем уравнений: метод подстановки и метод сложения |
|---|
| Справочник по тригонометрии |
• Тригонометрия прямоугольного треугольника • Тригонометрия произвольного треугольника • Тригонометрические формулы • Гиперболические функции |
|---|
| Справочник по исчислению |
• Формулы вычисления пределов • Производная числа • Общие производные • Производные показательных функций с основанием e • Производные простых тригонометрических функций • Правила вычисления производных • Первообразная (неопределённый интеграл) • Общие первообразные • Первообразные показательных функций от числа e • Правила вычисления первообразных • Определённые интегралы и основная теорема исчисления • Дифференциальные уравнения |
|---|
| Использование программы SPICE для моделирования электрических схем |
• Программа моделирования электрических цепей SPICE — Введение • История программы SPICE • Основы программирования в SPICE • Интерфейс командной строки • Компоненты электрических схем • Опции для проведения анализа • Странные особенности программы SPICE • Примеры электрических цепей и списков связей |
|---|
| Устранение неполадок – теория и практика |
• Вопросы, которые следует задать, прежде чем продолжить • Общие советы по устранению неполадок • Конкретные методы устранения неполадок • Вероятные сбои в проверенных системах • Вероятные сбои в непроверенных системах • Возможные ментальные ловушки |
|---|
| Схематические обозначения элементов цепи |
• Провода и соединения • Источники питания • Типы резисторов • Типы конденсаторов • Катушки индуктивности • Взаимные катушки индуктивности • Переключатели с ручным управлением • Управляемые процессом переключатели • Переключатели с электрическим приводом (реле) • Соединители • Диоды • Биполярные транзисторы • Переходные транзисторы с полевым эффектом (JFET) • Транзисторы с полевым эффектом с изолированным затвором (IGFET или MOSFET) • Гибридные транзисторы • Тиристоры • Интегральные схемы • Электронные лампы |
|---|
| Периодическая таблица химических элементов |
• Таблица Менделеева |
|---|
| Эксперименты |
|---|
| Введение |
• Электроника как точная наука • Обустраиваем домашнюю лабораторию |
|---|
| Основные концепции и испытательное оборудование |
• Использование вольтметра • Использование омметра • Очень простая схема • Использование амперметра при измерении силы тока • Закон Ома • Нелинейное сопротивление • Рассеяние мощности • Цепь с переключателем • Эксперимент по электромагнетизму • Эксперимент с электромагнитной индукцией |
|---|
| Электрические цепи постоянного тока |
• Электрические цепи постоянного тока – Введение • Последовательные источники питания • Параллельные источники питания • Делитель напряжения • Делитель тока • Потенциометр как делитель напряжения • Потенциометр как реостат • Прецизионный потенциометр • Ограничение диапазона реостата • Термоэлектричество • Мультиметр своими руками • Чувствительный детектор напряжения • Потенциометрический вольтметр • 4-проводное измерение сопротивления • Простейший компьютер • Картошка-батарейка • Зарядка и разрядка конденсатора • Индикатор скорости изменения |
|---|
| Электрические цепи переменного тока |
• Электрические цепи переменного тока – Введение • Трансформатор – блок питания • Сборка трансформатора • Переменный индуктор • Чувствительный аудиодетектор • Обнаружение магнитных полей переменного тока • Обнаружение электрических полей переменного тока • Альтернатор – автомобильный генератор • Асинхронный двигатель • Асинхронный двигатель побольше • Фазовый сдвиг • Погашение звука • Музыкальный синтезатор как генератор сигналов • ПК-осциллограф • Анализ волновых сигналов • Колебательный контур • Сигнальная связь |
|---|
| Дискретные полупроводниковые схемы |
• Дискретные полупроводниковые схемы – Введение • Коммутирующий диод • Полупериодный выпрямитель • Двухполупериодный мостовой выпрямитель • Двухполупериодный выпрямитель с центральным отводом • Цепь «выпрямитель/фильтр» • Регулятор напряжения • Транзистор как переключатель • Датчик статического электричества • Датчик импульсного света • Повторитель напряжения • Усилитель с общим эмиттером • Многокаскадный усилитель • Как построить схему токового зеркала • JFET – регулятор тока • Дифференциальный усилитель • Простой операционный усилитель • Аудио осциллограф • Ламповый аудио усилитель |
|---|
| Аналоговые интегральные схемы |
• Аналоговые интегральные схемы – Введение • Компаратор напряжения • Прецизионный повторитель напряжения • Неинвертирующий усилитель • Высокоимпедансный вольтметр • Интегратор • Аудио осциллограф на таймерной схеме 555 • Наклонный генератор на таймерной схеме 555 • ШИМ-контроллер мощности • Аудиоусилитель класса B |
|---|
| Цифровые интегральные схемы |
• Цифровые интегральные схемы – Введение • Основная функция вентилей • SR-защёлка на основе вентилей «ИЛИ-НЕ» • SR-защёлка на основе вентиля «И-НЕ» с входом разрешения • SR-триггер на основе вентиля «И-НЕ» • Светодиодный секвенсор • Простейший кодовый замок • 3-битный двоичный счётчик • 7-сегментный дисплей |
|---|
| Таймерные схемы 555 |
• Интегральный таймер 555 • Триггер Шмитта на интегральном таймере 555 • Гистерезисный осциллограф на интегральном таймере 555 • Моностабильный мультивибратор на интегральном таймере 555 • Минимальное количество комплектующих для КМОП-схемы 555 проблескового прибора длительного действия на красных светодиодах • КМОП-схема 555 проблескового прибора длительного действия на синих светодиодах • КМОП-схема 555 проблескового прибора длительного действия на светодиодах обратного хода • КМОП-схема 555 проблескового прибора длительного действия на красных светодиодах |
|---|