Электроника:Переменный ток/Многофазные цепи переменного тока/Гармоники в многофазных энергосистемах

Материал из Онлайн справочника
Перейти к навигацииПерейти к поиску

Перевод: Макаров В. (valemak)
Проверка/Оформление/Редактирование: Мякишев Е.А.


Гармоники в многофазных энергосистемах[1]

В главе 7 «Сигналы переменного тока смешанной частоты», мы исследовали концепцию гармоник в системах переменного тока: это частоты, которые являются целыми кратными основной (фундаментальной) частоте источника питания.

В системах питания переменного тока, в которых волна напряжения источника, поступающего от генератора переменного тока (альтернатор), должна быть одночастотной синусоидальной волной, неискажённой, без гармонических составляющих… идеальной, в общем.

Нелинейные компоненты в системах переменного тока

Это было бы так, если бы не нелинейные компоненты. Нелинейные компоненты потребляют ток непропорционально напряжению источника, вызывая несинусоидальные волны тока. Примеры нелинейных компонентов: газоразрядные лампы, полупроводниковые устройства управления мощностью (диоды, транзисторы, тиристоры, симисторы), трансформаторы (ток намагничивания первичной обмотки обычно не является синусоидальным из-за B/H-кривой насыщения сердечника) и электродвигатели (опять же, когда магнитные поля в сердечнике двигателя приближаются к уровню насыщения).

Даже лампы накаливания генерируют слегка несинусоидальные токи, поскольку сопротивление нити накала изменяется в течение всего цикла из-за быстрых колебаний температуры. Как мы узнали из главы, посвященной смешанным частотам, любое искажение синусоидальной формы волны означает наличие гармонических частот.

Когда в рассматриваемой несинусоидальной волне её части, находящиеся выше и ниже средней центральной линии, являются симметричными, то частоты гармоник будут только нечётными целыми числами, кратными основной частоте источника питания, чётные целые кратных будут отсутствовать.

Большинство нелинейных нагрузок генерируют именно такие волны тока, поэтому чётные гармоники (2-я, 4-я, 6-я, 8-я, 10-я, 12-я и т.д.) отсутствуют (или присутствуют минимально) в большинстве систем переменного тока.

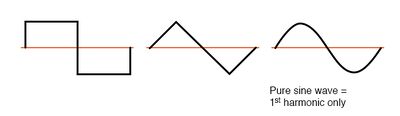
Рис. 1. Примеры симметричных сигналов – у таких будут только нечётные гармоники.

Примеры несимметричных сигналов (когда части волны, находящихся выше средней линии не являются зеркальным отображением частей, находящихся ниже средней линии) с присутствующими чётными гармониками:

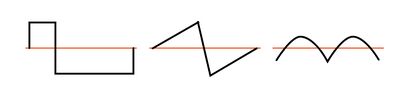
Рис. 2. Примеры несимметричных сигналов – у таких помимо нечётных также будут и выраженные чётные гармоники.

Несмотря на то, что половина возможных частот гармоник обычно нейтрализуется симметричным искажением нелинейных нагрузок, нечётные гармоники все же могут вызывать проблемы. Некоторые из этих проблем являются общими для всех энергосистем, хоть однофазных хоть многофазных.

Например, перегрев трансформатора из-за потерь на вихревые токи может произойти в любой энергосистеме переменного тока, в которой присутствует значительное количество гармоник.

Однако есть некоторые проблемы, вызванные гармоническими токами, которые характерны именно для многофазных систем питания, и как раз этим проблемам специально посвящён этот раздел.

SPICE-моделирование гармонических эффектов

Полезно иметь возможность моделировать нелинейные нагрузки в SPICE, чтобы не перегружать себя матаном и выработать интуитивное понимание гармонических эффектов.

Моделирование линейной системы переменного тока

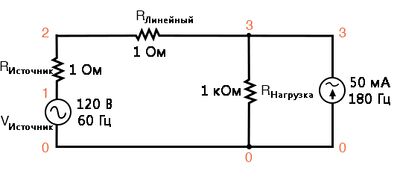
Во-первых, начнём наше моделирование с очень простой цепи переменного тока: одиночный источник синусоидального напряжения с чисто линейной нагрузкой и всеми соответствующими сопротивлениями:

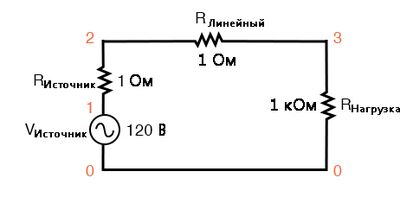
Рис. 3. Схема для SPICE с одним источником синусоидального сигнала.

Сопротивления RИсточник и RЛинейное в этой цепи – нечто большее, чем простая имитация реального мира: они также обеспечивают удобные сопротивления шунта для измерения токов в моделировании SPICE: путём считывания напряжения на сопротивлении 1 Ом, получаем прямое указание сколько тока здесь проходит, ибо E = IR (фактически сводится к E = I, т.к. R = 1 Ом).

Моделирование этой схемы в SPICE с анализом Фурье для напряжения, измеренного для RЛинейное, должно показать нам содержание гармоник в линейном токе этой схемы. С учётом данной схемы ток будет полностью линейным по своей природе, так что не ожидается никаких гармоник, кроме 1-й (фундаментальной) для частоты 60 Гц, если предположить, что частота источника равна 60 Гц.

linear load simulation
vsource 1 0 sin(0 120 60 0 0)
rsource 1 2 1
rline 2 3 1
rload 3 0 1k
.options itl5=0
.tran 0.5m 30m 0 1u
.plot tran v(2,3)
.four 60 v(2,3)
.end

Fourier components of transient response v(2,3) dc component = 4.028E-12

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.198E-01 1.000000 -72.000 0.000
2 1.200E+02 5.793E-12 0.000000 51.122 123.122
3 1.800E+02 7.407E-12 0.000000 -34.624 37.376
4 2.400E+02 9.056E-12 0.000000 4.267 76.267
5 3.000E+02 1.651E-11 0.000000 -83.461 -11.461
6 3.600E+02 3.931E-11 0.000000 36.399 108.399
7 4.200E+02 2.338E-11 0.000000 -41.343 30.657
8 4.800E+02 4.716E-11 0.000000 53.324 125.324
9 5.400E+02 3.453E-11 0.000000 21.691 93.691

total harmonic distortion = 0.000000 percent

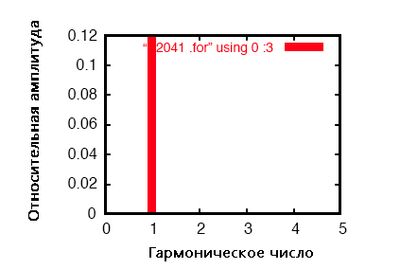
Рис. 4. График в частотной области одночастотного компонента.

Команда .plot обычно приводит к выводу синусоидального графика. В этом случае, однако, для краткости я намеренно опустил отображение формы сигнала – команда .plot нужна просто для того, чтобы удовлетворить специфическим требованиям программы SPICE при вызове функции для преобразования Фурье.

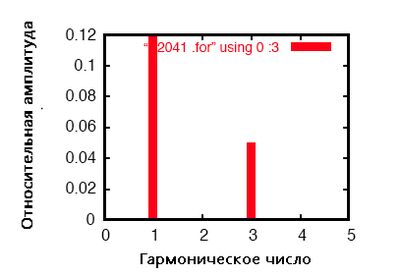
Никакое дискретное преобразование Фурье не является идеальным, и поэтому мы видим очень маленькие гармонические токи (находящиеся в диапазоне пико-ампер!) для всех частот вплоть до 9-й гармоники (это видно в результирующей таблице), что соответствует возможностям SPICE при выполнении анализа Фурье.

Мы показываем 0,1198 ампер (1.198E-01) для «составляющей Фурье» 1-й гармоники или основной частоты, которая является нашим ожидаемым током нагрузки: около 120 мА, при напряжении источника 120 В и сопротивлении нагрузки 1 кОм.

Простое моделирование нелинейной однофазной системы переменного тока

Попробуем теперь смоделировать нелинейную нагрузку, чтобы сгенерировать гармонические токи. Это можно сделать двумя принципиально разными способами. Один способ – спроектировать нагрузку с использованием нелинейных компонентов, таких как диоды или другие полупроводниковые устройства, с помощью SPICE они легко моделируются. Другой способ – добавить несколько источников переменного тока параллельно нагрузочному резистору.

Инженеры часто предпочитают второй метод для моделирования гармоник, поскольку источники тока известного значения лучше подходят для математического анализа сети, чем компоненты с очень сложными характеристиками отклика.

Поскольку мы перекладываем на SPICE всю математическую работу, сложность полупроводникового компонента не вызовет для нас проблем, но, поскольку источники тока можно точно настроить для получения любой произвольной величины тока (функция для этого весьма удобна), мы пойдём по второму пути:

Рис. 5. Схема для SPICE: источник питания на 60 Гц, что приводит к возникновению 3-й гармоники.
Nonlinear load simulation
vsource 1 0 sin(0 120 60 0 0)
rsource 1 2 1
rline 2 3 1
rload 3 0 1k
i3har 3 0 sin(0 50m 180 0 0)
.options itl5=0
.tran 0.5m 30m 0 1u
.plot tran v(2,3)
.four 60 v(2,3)
.end

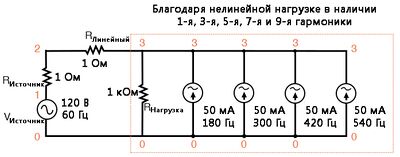
В этой схеме у нас есть источник тока величиной 50 мА и частотой 180 Гц, что в три раза превышает частоту источника 60 Гц. При подключении параллельно нагрузочному резистору 1 кОм его ток складывается с током резистора, создавая несинусоидальный общий линейный ток.

Приведу график волны напряжения, чтобы вы могли увидеть влияние тока третьей гармоники на общий ток, который обычно представляет собой простую синусоидальную волну.

Рис. 6. График SPICE во временно́й области, показывающий сложение частот 60 Гц источника питания и 180 Гц 3-й гармоники.

Fourier components of transient response v(2,3) dc component = 1.349E-11

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.198E-01 1.000000 -72.000 0.000
2 1.200E+02 1.609E-11 0.000000 67.570 139.570
3 1.800E+02 4.990E-02 0.416667 144.000 216.000
4 2.400E+02 1.074E-10 0.000000 -169.546 -97.546
5 3.000E+02 3.871E-11 0.000000 169.582 241.582
6 3.600E+02 5.736E-11 0.000000 140.845 212.845
7 4.200E+02 8.407E-11 0.000000 177.071 249.071
8 4.800E+02 1.329E-10 0.000000 156.772 228.772
9 5.400E+02 2.619E-10 0.000000 160.498 232.498

total harmonic distortion = 41.666663 percent

Рис. 7. График Фурье от SPICE, показывающий источник 60 Гц и 3-ю гармонику 180 Гц.

В этом анализе Фурье смешанные частоты представлены отдельно.

Здесь мы видим те же 0,1198 ампер тока 60 Гц (основная гармоника), что и в первом моделировании, но для 3-й гармоники мы видим 49,9 мА: при этом наш источник тока на 50 мА, 180 Гц. Почему только 49,9 а не все 50 мА?

Поскольку этот источник тока подключён к нагрузочному резистору 1 кОм, некоторые из его токов шунтируются (идут в обход) через нагрузку и не проходят обратно к источнику через линейный провод. Это неизбежное следствие моделирования такого типа, когда одна часть нагрузки является «нормальной» (резистор), а другая часть имитируется источником тока.

Моделирование нелинейной однофазной системы переменного тока с несколькими источниками тока

Если добавить больше источников тока к «нагрузке», то увидим дальнейшее искажение волны линейного тока, которая будет всё меньше напоминать идеальную синусоиду, и каждый из этих гармонических токов ломал бы анализ Фурье.

Рис. 8. Нелинейная нагрузка: присутствуют 1-я, 3-я, 5-я, 7-я и 9-я гармоники.
Nonlinear load simulation
vsource 1 0 sin(0 120 60 0 0)
rsource 1 2 1
rline 2 3 1
rload 3 0 1k
i3har 3 0 sin(0 50m 180 0 0)
i5har 3 0 sin(0 50m 300 0 0)
i7har 3 0 sin(0 50m 420 0 0)
i9har 3 0 sin(0 50m 540 0 0)
.options itl5=0
.tran 0.5m 30m 0 1u
.plot tran v(2,3)
.four 60 v(2,3)
.end

Fourier components of transient response v(2,3) dc component = 6.299E-11

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.198E-01 1.000000 -72.000 0.000
2 1.200E+02 1.900E-09 0.000000 -93.908 -21.908
3 1.800E+02 4.990E-02 0.416667 144.000 216.000
4 2.400E+02 5.469E-09 0.000000 -116.873 -44.873
5 3.000E+02 4.990E-02 0.416667 0.000 72.000
6 3.600E+02 6.271E-09 0.000000 85.062 157.062
7 4.200E+02 4.990E-02 0.416666 -144.000 -72.000
8 4.800E+02 2.742E-09 0.000000 -38.781 33.219
9 5.400E+02 4.990E-02 0.416666 72.000 144.000

total harmonic distortion = 83.333296 percent

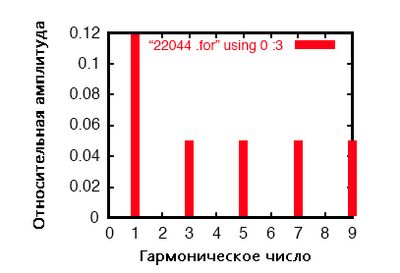
Рис. 9. Как видно из анализа Фурье, каждый источник гармонического тока одинаково представлен в линейном токе, по 49,9 мА каждый. Пока это просто моделирование однофазной энергосистемы.

Моделирование трёхфазной системы переменного тока

Все становится интереснее в трёхфазном моделировании. Будут выполнены два анализа Фурье: один для напряжения на линейном резисторе, а второй – для напряжения на нейтральном резисторе.

Как и прежде, считывание напряжений на фиксированных сопротивлениях в 1 Ом каждое даёт прямые показания тока, протекающего через эти резисторы (из-за того, что соответствующие R = 1 Ом).

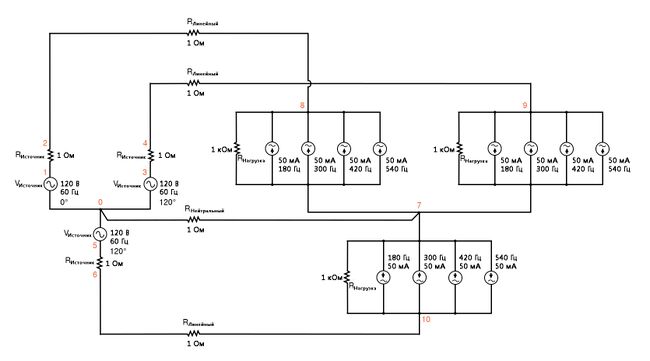
Рис. 10. Схема для SPICE: анализ «линейного тока» и «нейтрального тока», 4-проводная YY-система (и система источников питания и нагрузка с гармониками соединены в Y-конфигурации).
Y-Y source/load 4-wire system with harmonics
*
* фаза 1 напряжение и сопротивление источника питания (120 В /_ 0 градусов)
vsource1 1 0 sin(0 120 60 0 0)
rsource1 1 2 1
*
* фаза 2 напряжение и сопротивление источника питания (120 В /_ 120 градусов)
vsource2 3 0 sin(0 120 60 5.55555m 0)
rsource2 3 4 1
*
* фаза 3 напряжение и сопротивление источника питания (120 v /_ 240 градусов)
vsource3 5 0 sin(0 120 60 11.1111m 0)
rsource3 5 6 1
*
* сопротивления линейных и нейтрального проводов
rline1 2 8 1
rline2 4 9 1
rline3 6 10 1
rneutral 0 7 1
*
* фаза 1 нагрузки
rload1 8 7 1k
i3har1 8 7 sin(0 50m 180 0 0)
i5har1 8 7 sin(0 50m 300 0 0)
i7har1 8 7 sin(0 50m 420 0 0)
i9har1 8 7 sin(0 50m 540 0 0)
*
* фаза 2 нагрузки
rload2 9 7 1k
i3har2 9 7 sin(0 50m 180 5.55555m 0)
i5har2 9 7 sin(0 50m 300 5.55555m 0)
i7har2 9 7 sin(0 50m 420 5.55555m 0)
i9har2 9 7 sin(0 50m 540 5.55555m 0)
*
* фаза 3 нагрузки
rload3 10 7 1k
i3har3 10 7 sin(0 50m 180 11.1111m 0)
i5har3 10 7 sin(0 50m 300 11.1111m 0)
i7har3 10 7 sin(0 50m 420 11.1111m 0)
i9har3 10 7 sin(0 50m 540 11.1111m 0)
*
* Результаты анализа
.options itl5=0
.tran 0.5m 100m 12m 1u
.plot tran v(2,8)
.four 60 v(2,8)
.plot tran v(0,7)
.four 60 v(0,7)
.end

Анализ Фурье линейного тока:

Fourier components of transient response v(2,8) dc component = -6.404E-12

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.198E-01 1.000000 0.000 0.000
2 1.200E+02 2.218E-10 0.000000 172.985 172.985
3 1.800E+02 4.975E-02 0.415423 0.000 0.000
4 2.400E+02 4.236E-10 0.000000 166.990 166.990
5 3.000E+02 4.990E-02 0.416667 0.000 0.000
6 3.600E+02 1.877E-10 0.000000 -147.146 -147.146
7 4.200E+02 4.990E-02 0.416666 0.000 0.000
8 4.800E+02 2.784E-10 0.000000 -148.811 -148.811
9 5.400E+02 4.975E-02 0.415422 0.000 0.000

total harmonic distortion = 83.209009 percent

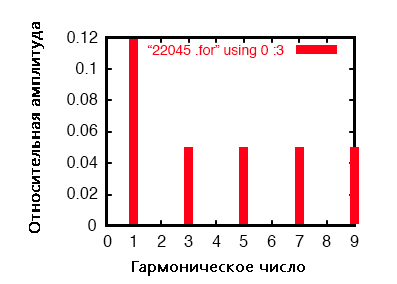
Рис. 11. Анализ Фурье линейного тока в сбалансированной YY-системе.

Анализ Фурье нейтрального тока:

Fourier components of transient response v(0,7) dc component = 1.819E-10

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 4.337E-07 1.000000 60.018 0.000
2 1.200E+02 1.869E-10 0.000431 91.206 31.188
3 1.800E+02 1.493E-01 344147.7638 -180.000 -240.018
4 2.400E+02 1.257E-09 0.002898 -21.103 -81.121
5 3.000E+02 9.023E-07 2.080596 119.981 59.963
6 3.600E+02 3.396E-10 0.000783 15.882 -44.136
7 4.200E+02 1.264E-06 2.913955 59.993 -0.025
8 4.800E+02 5.975E-10 0.001378 35.584 -24.434
9 5.400E+02 1.493E-01 344147.4889 -179.999 -240.017
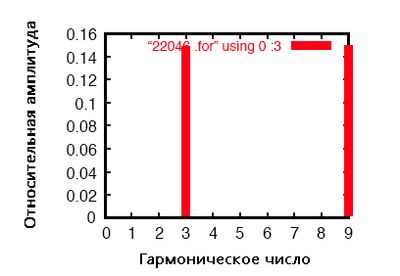
Рис. 12. Анализ Фурье нейтрального тока не показывает никаких гармоник! Сравните с анализом Фурье линейного тока из предыдущего примера.

Это сбалансированная система питания YY, каждая фаза которой идентична однофазной системе переменного тока, смоделированной ранее. Следовательно, неудивительно, что анализ Фурье для линейного тока в одной фазе трёхфазной системы почти идентичен анализу Фурье для линейного тока в однофазной системе, где основной (60 Гц) линейный ток 0,1198 ампер и токи нечётных гармоник примерно 50 мА каждый.

Что здесь удивительно, так это анализ тока нейтрального проводника, который определяется падением напряжения на RНейтральный между узлами 0 и 7 в схеме для SPICE. В сбалансированной трёхфазной нагрузке Y-схемы мы ожидаем нулевой ток в нейтральном проводе. Все фазные токи – которые сами по себе проходят через нейтральный провод обратно к фазе питания на источнике Y – должны нейтрализовать друг друга по отношению к нейтральному проводнику, потому что все они одинаковой величины и все смещены на 120° относительно друг друга.

В системе без гармонических токов именно так и происходит: нулевой ток через нейтральный провод.

Эффекты гармонических токов в системе

Однако нельзя сказать то же самое, если в той же системе будут присутствовать гармонические токи.

Обратите внимание, что ток основной частоты (60 Гц или 1-я гармоника) практически отсутствует в нейтральном проводе. Наш анализ Фурье показывает только 0,4337 мкА первой гармоники при считывании напряжения на RНейтральный. То же самое можно сказать о 5-й и 7-й гармониках, причём оба этих тока имеют незначительную величину.

Напротив, 3-я и 9-я гармоники сильно представлены в нейтральном проводе, по 149,3 мА (1,493E-01 вольт на 1 Ом) каждая! Это почти 150 мА, или в три раза больше значений источников тока по отдельности.

С тремя источниками на каждую гармоническую частоту в нагрузке, кажется, что наши токи 3-й и 9-й гармоник в каждой фазе складываются, образуя ток в нейтральном проводе.

Анализ графиков во временно́й области

Это именно то, что происходит, хотя, возможно, это кому-то покажется неочевидным.

Ключ к пониманию явствует из графика фазовых токов во временно́й области. Взгляните на этот график сбалансированных фазных токов во времени с последовательностью фаз 1-2-3:

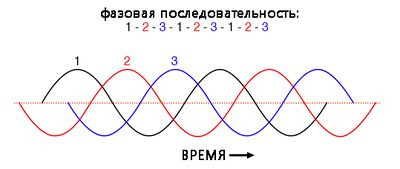
Рис. 13. Последовательность фаз 1-2-3-1-2-3-1-2-3 равноотстоящих друг от друга волн.

На примере этих трёх основных волн, одинаково смещённых по временно́й оси графика, легко увидеть, как они компенсируют друг друга, давая результирующий нулевой ток в нейтральном проводнике. Однако давайте рассмотрим, как будет выглядеть волна 3-й гармоники для фазы 1, наложенной на график:

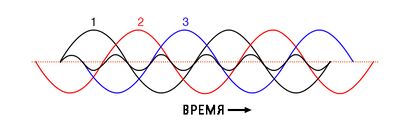
Рис. 14. Волна 3-й гармоники для фазы 1 наложена на волны трёхфазной основной частоты.

Обратите внимание на то, что эта гармоническая волна имеет такое же фазовое соотношение со 2-й и 3-ей основными волнами, как и с 1-й: в каждом положительном полупериоде любой из основных волн вы найдёте ровно два положительных полупериода и одну отрицательную половину – таков цикл гармонической волны.

Это означает, что волны 3-й гармоники всех трёх сигналов основной частоты с фазовым сдвигом на 120° фактически находятся в фазе и друг с другом. Значение фазового сдвига 120°, обычно принимаемое в трёхфазных системах переменного тока, применяется только к основным частотам, а не к их гармоническим кратным!

Если бы мы для трёх основных волн изобразили все их три третьи гармоники на одном графике, то увидели, что они точно накладываются друг на друга и выглядели бы как единая унифицированная волна (на графике выделена жирной чёрной линией):

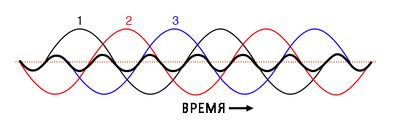
Рис. 15. Третьи гармоники для фаз 1, 2, 3 все совпадают при наложении на основные формы трёхфазных сигналов.

Математический анализ графика во временно́й области

Для тех, кто предпочитает язык математики этот принцип можно выразить символически. Предположим, что A представляет один сигнал, а B – другой, оба имеют одинаковую частоту, но сдвинуты по фазе на 120° относительно друг от друга. Назовем 3-ю гармонику каждого сигнала A' и B' соответственно.

Фазовый сдвиг между A' и B' не равен 120° (то есть не равен сдвигу фаз между А и В). Однако, чтобы выяснить эти фазовые сдвиги, нужно в 3 раза увеличить фазовые сдвиги соответствующих родительских волн. На графике видно, что волны A' и B' в три раза быстрее, чем A и B. Сдвиг между волнами точно выражается в терминах фазового угла только в том случае, если предполагается одинаковая угловая скорость.

При связывании сигналов с разной частотой наиболее точный способ представления фазового сдвига – это время; а временно́й сдвиг между A' и B' эквивалентен 120° при частоте в три раза меньшей или 360° при частоте A' и B'. Фазовый сдвиг на 360° совпадает с фазовым сдвигом на 0°, то есть без фазового сдвига вообще.

Таким образом, A' и B' должны находиться в фазе друг с другом:

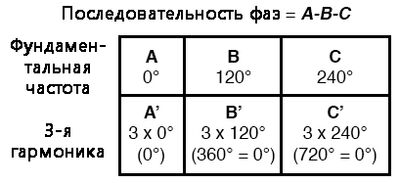
Рис. 16. Последовательность фаз A, B и C.

Эта характеристика 3-й гармоники в трёхфазной системе также справедлива для любых целых кратных 3-й гармоники.

Таким образом, не только все третьи гармоники всех основных волн находятся в фазе друг с другом, но также это касается всех шестых гармоник всех основных волн (потому что 6 кратно трём), всех девятых гармоник всех основных волн (потому что 9 кратно трём), всех 12-х гармоник, всех 15-х гармоник, всех 18-х гармоник, всех 21-х гармоник и так далее.

Поскольку только нечётные гармоники появляются в системах, в которых искажение волны симметрично относительно центральной средней оси, а большинство нелинейных нагрузок создают симметричное искажение, чётные кратные 3-й гармоники (гармоники 6-я, 12-я, 18-я и прочие кратные трём) вносят значительный вклад в ток нейтрального провода.

В многофазных энергосистемах с другим количеством фаз, отличным от трёх, этот эффект возникает с гармониками того же кратного числа. При этом фазовый сдвиг вычисляется как 360° делённое на количество фаз. Например, гармонические токи, которые добавляются в нейтральный провод 4-фазной «звездообразной» системы, имеют фазовый сдвиг между основными формами волны 90° (= 360°/4), и имеют порядковые гармонические номера 4, 8, 12, 16, 20 и т. д. (потому что все эти числа кратны четырём).

Тройные гармоники

Из-за распространённости и значимости в трёхфазных энергосистемах 3-я гармоника и её кратные имеют собственное особое название: тройные гармоники.

Все тройные гармоники складываются друг с другом в нейтральном проводе 4-проводной нагрузки с Y-соединением. В энергосистемах со значительной нелинейной нагрузкой тройные гармонические токи могут быть достаточно большими, чтобы вызвать перегрев нейтральных проводников.

Это большая проблема, поскольку по другим соображениям безопасности нейтральным проводникам нельзя иметь максимальную токовую защиту, и поэтому нет никаких условий для автоматического отключения системы в случае возникновения сверхтоков в нейтральном проводнике.

Анализ влияния тройных гармоник в цепи YY

На следующем рисунке показано, как тройные гармонические токи, создаваемые нагрузкой, складываются в нейтральном проводнике. Символ «ω» используется для обозначения угловой скорости и математически эквивалентен 2πf. Таким образом, «ω» представляет основную частоту, «3ω» представляет 3-ю гармонику, «5ω» представляет 5-ю гармонику и так далее:

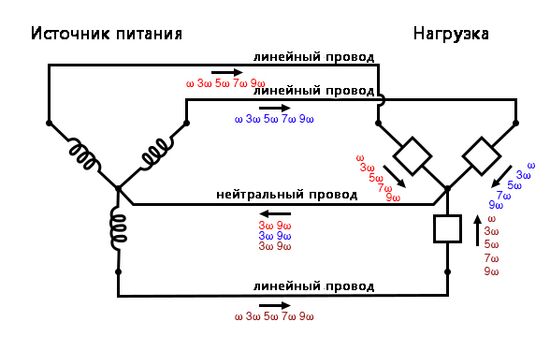
Рис. 17. «YY»: гармонические токи складываются в нейтральном проводе.

Из-за этих нежелательных дополнительных тройных (т.е. создаваемых тройными гармониками) токов возникает соблазн вообще отказаться от нейтрального провода. Если нет нейтрального провода, в котором могут протекать тройные токи, то тогда и тройных токов не будет, ведь так?

К сожалению, это вызывает другую проблему: центральная точка нагрузки Y-конфигурации больше не будет иметь тот же потенциал, что и источник питания, а это означает, что каждая фаза нагрузки будет получать напряжение, отличное от того, которое вырабатывается источником питания.

Давайте повторно запустим предыдущую симуляцию SPICE, только без RНейтральный = 1 Ом и посмотрим, что произойдёт:

Y-Y source/load (no neutral) with harmonics
*
* фаза 1 напряжение и сопротивление источника питания (120 v / 0 градусов)
vsource1 1 0 sin(0 120 60 0 0)
rsource1 1 2 1
*
* фаза 2 напряжение и сопротивление источника питания (120 v / 120 градусов)
vsource2 3 0 sin(0 120 60 5.55555m 0)
rsource2 3 4 1
*
* фаза 3 напряжение и сопротивление источника питания (120 v / 240 градусов)
vsource3 5 0 sin(0 120 60 11.1111m 0)
rsource3 5 6 1
*
* сопротивления линейных проводов
rline1 2 8 1
rline2 4 9 1
rline3 6 10 1
*
* фаза 1 нагрузки
rload1 8 7 1k
i3har1 8 7 sin(0 50m 180 0 0)
i5har1 8 7 sin(0 50m 300 0 0)
i7har1 8 7 sin(0 50m 420 0 0)
i9har1 8 7 sin(0 50m 540 0 0)
*
* фаза 2 нагрузки
rload2 9 7 1k
i3har2 9 7 sin(0 50m 180 5.55555m 0)
i5har2 9 7 sin(0 50m 300 5.55555m 0)
i7har2 9 7 sin(0 50m 420 5.55555m 0)
i9har2 9 7 sin(0 50m 540 5.55555m 0)
*
* фаза 3 нагрузки
rload3 10 7 1k
i3har3 10 7 sin(0 50m 180 11.1111m 0)
i5har3 10 7 sin(0 50m 300 11.1111m 0)
i7har3 10 7 sin(0 50m 420 11.1111m 0)
i9har3 10 7 sin(0 50m 540 11.1111m 0)
*
* результаты анализа
.options itl5=0
.tran 0.5m 100m 12m 1u
.plot tran v(2,8)
.four 60 v(2,8)
.plot tran v(0,7)
.four 60 v(0,7)
.plot tran v(8,7)
.four 60 v(8,7)
.end

Анализ Фурье линейного тока:

Fourier components of transient response v(2,8) dc component = 5.423E-11

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.198E-01 1.000000 0.000 0.000
2 1.200E+02 2.388E-10 0.000000 158.016 158.016
3 1.800E+02 3.136E-07 0.000003 -90.009 -90.009
4 2.400E+02 5.963E-11 0.000000 -111.510 -111.510
5 3.000E+02 4.990E-02 0.416665 0.000 0.000
6 3.600E+02 8.606E-11 0.000000 -124.565 -124.565
7 4.200E+02 4.990E-02 0.416668 0.000 0.000
8 4.800E+02 8.126E-11 0.000000 -159.638 -159.638
9 5.400E+02 9.406E-07 0.000008 -90.005 -90.005

total harmonic distortion = 58.925539 percent

Анализ Фурье для напряжения между двумя центральными точками «Y»:

Fourier components of transient response v(0,7) dc component = 6.093E-08

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.453E-04 1.000000 60.018 0.000
2 1.200E+02 6.263E-08 0.000431 91.206 31.188
3 1.800E+02 5.000E+01 344147.7879 -180.000 -240.018
4 2.400E+02 4.210E-07 0.002898 -21.103 -81.121
5 3.000E+02 3.023E-04 2.080596 119.981 59.963
6 3.600E+02 1.138E-07 0.000783 15.882 -44.136
7 4.200E+02 4.234E-04 2.913955 59.993 -0.025
8 4.800E+02 2.001E-07 0.001378 35.584 -24.434
9 5.400E+02 5.000E+01 344147.4728 -179.999 -240.017

total harmonic distortion = ************ percent

Анализ Фурье для напряжения фазы нагрузки:

Fourier components of transient response v(8,7) dc component = 6.070E-08

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.198E+02 1.000000 0.000 0.000
2 1.200E+02 6.231E-08 0.000000 90.473 90.473
3 1.800E+02 5.000E+01 0.417500 -180.000 -180.000
4 2.400E+02 4.278E-07 0.000000 -19.747 -19.747
5 3.000E+02 9.995E-02 0.000835 179.850 179.850
6 3.600E+02 1.023E-07 0.000000 13.485 13.485
7 4.200E+02 9.959E-02 0.000832 179.790 179.789
8 4.800E+02 1.991E-07 0.000000 35.462 35.462
9 5.400E+02 5.000E+01 0.417499 -179.999 -179.999

total harmonic distortion = 59.043467 percent

Действительно, происходят что-то странное.

Во-первых, мы видим, что тройные гармонические токи (3-я и 9-я) почти исчезают в линейных проводах, соединяющих нагрузку с соответствующим источником. Токи 5-й и 7-й гармоник присутствуют на своих нормальных уровнях (приблизительно 50 мА), но токи 3-й и 9-й гармоник имеют незначительную величину.

Во-вторых, мы видим, что существует значительная гармоническая составляющая напряжения между двумя центральными точками Y-конфигурации, между которыми используется нейтральный проводник. Согласно SPICE, между этими двумя точками 50 вольт частоты как 3-й, так и 9-й гармоник, что определённо ненормально для линейной (без гармоник) сбалансированной Y-системы.

Наконец, напряжение, измеренное на одной из фаз нагрузки (между узлами 8 и 7 в схеме для анализа SPICE), также показывает сильные тройные гармонические напряжения по 50 вольт каждая.

На рисунке ниже графически представлены вышеупомянутые эффекты.

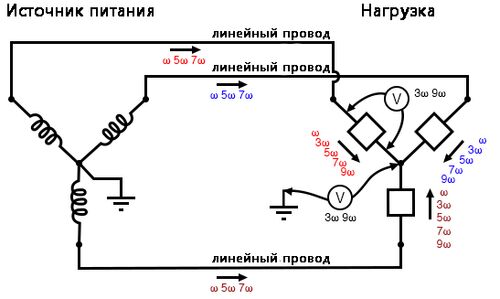
Рис. 18. Трёхпроводная система «YY» (без нейтрального провода): между центрами Y-конфигурации появляются тройные (гармонические) напряжения. На фазах нагрузки появляются тройные (гармонические) напряжения. А вот в линейных проводниках тройные (гармонические) токи не возникают.

Таким образом, удаление нейтрального провода приводит к «горячей» центральной точке нагрузки Y-конфигурации, а также к гармоническим фазовым напряжениям нагрузки равной величины, состоящим из тройных (гармонических) частот.

В предыдущем моделировании, где у нас была 4-проводная система с Y-соединением, нежелательным эффектом от гармоник был чрезмерный ток в нейтральном проводе, но по крайней мере каждая фаза нагрузки получала напряжение, почти не содержащее гармоник.

Анализ влияния тройных гармоник в схеме Δ-Y

Поскольку удаление нейтрального провода, похоже, не устранило проблемы, вызванные гармониками, возможно, переключение на конфигурацию Δ сработает? Давайте попробуем для источника схему Δ вместо Y, сохраняя нагрузку в её нынешней Y-конфигурации, и посмотрим, что произойдёт.

Измеряемыми параметрами будут линейный ток (напряжение на RЛинейный, узлы 0 и 8), напряжение фазы нагрузки (узлы 8 и 7) и ток фазы источника (напряжение на RИсточник, узлы 1 и 2).

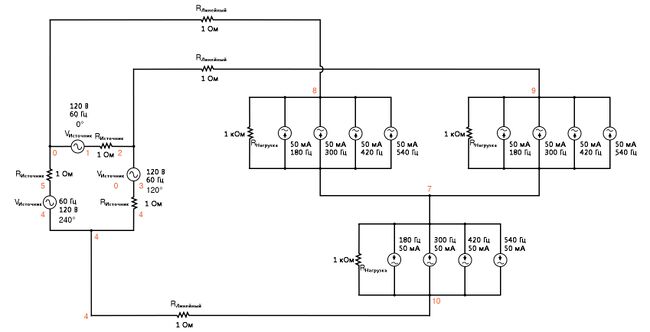
Рис. 19. Источник/нагрузка в системе «дельта-звезда» с гармониками.
Delta-Y source/load with harmonics
*
* фаза 1 напряжение и сопротивление источника питания (120 v /_ 0 градусов)
vsource1 1 0 sin(0 207.846 60 0 0)
rsource1 1 2 1
*
* фаза 2 напряжение и сопротивление источника питания (120 v /_ 120 градусов)
vsource2 3 2 sin(0 207.846 60 5.55555m 0)
rsource2 3 4 1
*
* фаза 3 напряжение и сопротивление источника питания (120 v /_ 240 градусов)
vsource3 5 4 sin(0 207.846 60 11.1111m 0)
rsource3 5 0 1
*
* сопротивления линейных проводов
rline1 0 8 1
rline2 2 9 1
rline3 4 10 1
*
* фаза 1 нагрузки
rload1 8 7 1k
i3har1 8 7 sin(0 50m 180 9.72222m 0)
i5har1 8 7 sin(0 50m 300 9.72222m 0)
i7har1 8 7 sin(0 50m 420 9.72222m 0)
i9har1 8 7 sin(0 50m 540 9.72222m 0)
*
* фаза 2 нагрузки
rload2 9 7 1k
i3har2 9 7 sin(0 50m 180 15.2777m 0)
i5har2 9 7 sin(0 50m 300 15.2777m 0)
i7har2 9 7 sin(0 50m 420 15.2777m 0)
i9har2 9 7 sin(0 50m 540 15.2777m 0)
*
* фаза 3 нагрузки
rload3 10 7 1k
i3har3 10 7 sin(0 50m 180 4.16666m 0)
i5har3 10 7 sin(0 50m 300 4.16666m 0)
i7har3 10 7 sin(0 50m 420 4.16666m 0)
i9har3 10 7 sin(0 50m 540 4.16666m 0)
*
* результаты анализа
.options itl5=0
.tran 0.5m 100m 16m 1u
.plot tran v(0,8) v(8,7) v(1,2)
.four 60 v(0,8) v(8,7) v(1,2)
.end

Примечание: следующий абзац предназначен для тех любопытствующих, что отслеживают все детали в листингах моих программ для SPICE. Если вы просто хотите узнать, что же происходит в цепи, то несколько абзацев пояснительного текста к программе можете смело пропустить!

Если в моделируемой цепи есть источники питания переменного тока разной частоты и разной фазы, единственный способ задать это в программе SPICE – настроить источники питания с временем задержки или сдвигом фазы, указанным в секундах. Таким образом, источник 0° имеет пять определяющих цифр: «(0 207,846 60 0 0)», что означает «смещение 0 вольт постоянного тока, пиковая амплитуда 207,846 вольт (120 умноженное на квадратный корень из трёх, чтобы гарантировать, что напряжения фазы нагрузки остаются на уровне 120 В каждый), 60 Гц, 0 задержки времени и 0 коэффициента демпфирования.

Источник с фазовым сдвигом на 120° имеет следующие значения: «(0 207,846 60 5,55555m 0)», всё то же самое, что и для первого, за исключением фактора временно́й задержки 5,55555 миллисекунд, или 1/3 от полного периода 16,6667 миллисекунд для волны с частотой 60 Гц.

Источник 240° должен иметь временну́ю задержку вдвое больше, что эквивалентно доле 240/360 от 16,6667 миллисекунд, что составляет 11,1111 миллисекунд.

Это для источника, с Δ-схемой соединения. С другой стороны, нагрузка, соединённая по схеме Y, требует другого набора значений задержки времени для источников гармонического тока, поскольку фазные напряжения в нагрузке Y не совпадают по фазе с фазными напряжениями источника Δ.

Если напряжения источника Δ VAC, VBA и VCB относятся к 0°, 120° и 240°, соответственно, то напряжения нагрузки «Y» VA, VB и VC будут иметь фазовые углы -30°, 90° и 210° соответственно.

Это универсальное свойство всех схем Δ-Y, а не прихоть программы SPICE. Поэтому, когда я указал время задержки для источников гармоник, мне пришлось установить их на 15,2777 миллисекунды (-30° или + 330°), 4,16666 миллисекунды (90°) и 9,72222 миллисекунды (210°).

И последнее замечание: при задержке источников переменного тока в SPICE они не «включаются», пока не истечёт время их задержки, что означает, что любой математический анализ до этого момента времени будет ошибочным. С учётом этого, я настроил в строке анализа переходных процессов .tran таким образом, чтобы анализ совершался с задержкой до 16 миллисекунд после запуска, что даёт всем источникам в списке соединений время для включения до того, как будет произведён какой-либо анализ.

Результат этого анализа почти так же неутешителен, как и предыдущий (см. рисунок ниже). Линейные токи остаются неизменными (единственной существенной составляющей гармоник являются 5-я и 7-я гармоники), и напряжения фазы нагрузки также остаются неизменными, с полными 50 вольтами тройных гармоник (3-я и 9-я) частот на каждом компоненте нагрузки.

Фазовый ток источника является частью линейного тока, что неудивительно. Здесь представлены как 5-я, так и 7-я гармоники, с незначительными тройными гармониками:

Анализ Фурье линейного тока:

Fourier components of transient response v(0,8) dc component = -6.850E-11

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.198E-01 1.000000 150.000 0.000
2 1.200E+02 2.491E-11 0.000000 159.723 9.722
3 1.800E+02 1.506E-06 0.000013 0.005 -149.996
4 2.400E+02 2.033E-11 0.000000 52.772 -97.228
5 3.000E+02 4.994E-02 0.416682 30.002 -119.998
6 3.600E+02 1.234E-11 0.000000 57.802 -92.198
7 4.200E+02 4.993E-02 0.416644 -29.998 -179.998
8 4.800E+02 8.024E-11 0.000000 -174.200 -324.200
9 5.400E+02 4.518E-06 0.000038 -179.995 -329.995

total harmonic distortion = 58.925038 percent

Анализ Фурье напряжения фазы нагрузки:

Fourier components of transient response v(8,7) dc component = 1.259E-08

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.198E+02 1.000000 150.000 0.000
2 1.200E+02 1.941E-07 0.000000 49.693 -100.307
3 1.800E+02 5.000E+01 0.417222 -89.998 -239.998
4 2.400E+02 1.519E-07 0.000000 66.397 -83.603
5 3.000E+02 6.466E-02 0.000540 -151.112 -301.112
6 3.600E+02 2.433E-07 0.000000 68.162 -81.838
7 4.200E+02 6.931E-02 0.000578 148.548 -1.453
8 4.800E+02 2.398E-07 0.000000 -174.897 -324.897
9 5.400E+02 5.000E+01 0.417221 90.006 -59.995

total harmonic distortion = 59.004109 percent

Анализ Фурье фазного тока источника: Fourier components of transient response v(1,2) dc component = 3.564E-11

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 6.906E-02 1.000000 -0.181 0.000
2 1.200E+02 1.525E-11 0.000000 -156.674 -156.493
3 1.800E+02 1.422E-06 0.000021 -179.996 -179.815
4 2.400E+02 2.949E-11 0.000000 -110.570 -110.390
5 3.000E+02 2.883E-02 0.417440 -179.996 -179.815
6 3.600E+02 2.324E-11 0.000000 -91.926 -91.745
7 4.200E+02 2.883E-02 0.417398 -179.994 -179.813
8 4.800E+02 4.140E-11 0.000000 -39.875 -39.694
9 5.400E+02 4.267E-06 0.000062 0.006 0.186

total harmonic distortion = 59.031969 percent

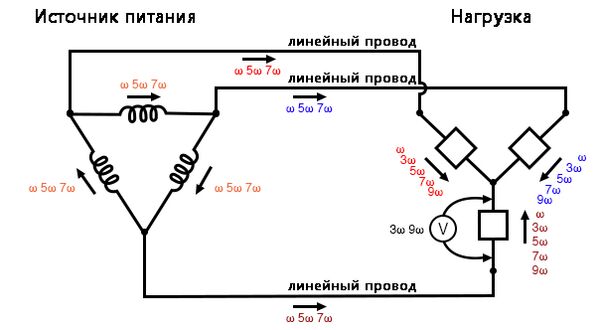
Рис. 20. Источник/нагрузка в системе «Δ-Y»: в фазах нагрузки появляются тройные (гармонические) напряжения. В линейных проводниках и в фазных обмотках источника тройные (гармонические) токи не возникают.

На самом деле, единственное преимущество конфигурации Δ-Y с точки зрения гармоник состоит в том, что больше нет центральной точки на нагрузке, представляющей опасность поражения электрическим током. В противном случае компоненты нагрузки получают такие же богатые гармониками напряжения, а линии имеют те же токи, что и в трёхпроводной Y-системе.

Анализ влияния тройных гармоник в схеме Δ-Δ

Если переконфигурировать систему в схему Δ-Δ (как на рисунке ниже), это гарантирует, что каждый компонент нагрузки получает негармоническое напряжение, поскольку каждая фаза нагрузки напрямую подключена параллельно каждой фазе источника.

Полное отсутствие каких-либо нейтральных проводов или «центральных точек» в системе Δ-Δ предотвращает возникновение странных напряжений или дополнительных токов. Казалось бы, вот оно – идеальное решение. Давайте смоделируем и понаблюдаем, анализируя линейный ток, напряжение фазы нагрузки и ток фазы источника:

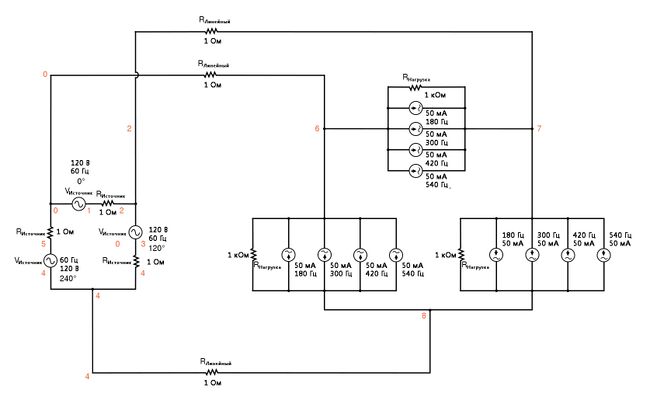
Рис. 21. Источник/нагрузка по схеме Δ-Δ с гармониками.
Delta-Delta source/load with harmonics
*
* фаза 1 напряжение и сопротивление источника питания (120 v /_ 0 градусов)
vsource1 1 0 sin(0 120 60 0 0)
rsource1 1 2 1
*
* фаза 2 напряжение и сопротивление источника питания (120 v /_ 120 градусов)
vsource2 3 2 sin(0 120 60 5.55555m 0)
rsource2 3 4 1
*
* фаза 3 напряжение и сопротивление источника питания (120 v /_ 240 градусов)
vsource3 5 4 sin(0 120 60 11.1111m 0)
rsource3 5 0 1
*
* сопротивления линейных проводов
rline1 0 6 1
rline2 2 7 1
rline3 4 8 1
*
* фаза 1 нагрузки
rload1 7 6 1k
i3har1 7 6 sin(0 50m 180 0 0)
i5har1 7 6 sin(0 50m 300 0 0)
i7har1 7 6 sin(0 50m 420 0 0)
i9har1 7 6 sin(0 50m 540 0 0)
*
* фаза 2 нагрузки
rload2 8 7 1k
i3har2 8 7 sin(0 50m 180 5.55555m 0)
i5har2 8 7 sin(0 50m 300 5.55555m 0)
i7har2 8 7 sin(0 50m 420 5.55555m 0)
i9har2 8 7 sin(0 50m 540 5.55555m 0)
*
* фаза 3 нагрузки
rload3 6 8 1k
i3har3 6 8 sin(0 50m 180 11.1111m 0)
i5har3 6 8 sin(0 50m 300 11.1111m 0)
i7har3 6 8 sin(0 50m 420 11.1111m 0)
i9har3 6 8 sin(0 50m 540 11.1111m 0)
*
* результаты анализа
.options itl5=0
.tran 0.5m 100m 16m 1u
.plot tran v(0,6) v(7,6) v(2,1) i(3har1)
.four 60 v(0,6) v(7,6) v(2,1)
.end

Анализ Фурье линейного тока:

Fourier components of transient response v(0,6) dc component = -6.007E-11

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 2.070E-01 1.000000 150.000 0.000
2 1.200E+02 5.480E-11 0.000000 156.666 6.666
3 1.800E+02 6.257E-07 0.000003 89.990 -60.010
4 2.400E+02 4.911E-11 0.000000 8.187 -141.813
5 3.000E+02 8.626E-02 0.416664 -149.999 -300.000
6 3.600E+02 1.089E-10 0.000000 -31.997 -181.997
7 4.200E+02 8.626E-02 0.416669 150.001 0.001
8 4.800E+02 1.578E-10 0.000000 -63.940 -213.940
9 5.400E+02 1.877E-06 0.000009 89.987 -60.013

total harmonic distortion = 58.925538 percent

Анализ Фурье напряжения фазы нагрузки:

Fourier components of transient response v(7,6) dc component = -5.680E-10

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.195E+02 1.000000 0.000 0.000
2 1.200E+02 1.039E-09 0.000000 144.749 144.749
3 1.800E+02 1.251E-06 0.000000 89.974 89.974
4 2.400E+02 4.215E-10 0.000000 36.127 36.127
5 3.000E+02 1.992E-01 0.001667 -180.000 -180.000
6 3.600E+02 2.499E-09 0.000000 -4.760 -4.760
7 4.200E+02 1.992E-01 0.001667 -180.000 -180.000
8 4.800E+02 2.951E-09 0.000000 -151.385 -151.385
9 5.400E+02 3.752E-06 0.000000 89.905 89.905

total harmonic distortion = 0.235702 percent

Анализ Фурье фазного тока источника:

Fourier components of transient response v(2,1) dc component = -1.923E-12

harmonic
no		 frequency
(hz)		 Fourier
component		 normalized
component		 phase
(deg)		 normalized
phase (deg)
1 6.000E+01 1.194E-01 1.000000 179.940 0.000
2 1.200E+02 2.569E-11 0.000000 133.491 -46.449
3 1.800E+02 3.129E-07 0.000003 89.985 -89.955
4 2.400E+02 2.657E-11 0.000000 23.368 -156.571
5 3.000E+02 4.980E-02 0.416918 -180.000 -359.939
6 3.600E+02 4.595E-11 0.000000 -22.475 -202.415
7 4.200E+02 4.980E-02 0.416921 -180.000 -359.939
8 4.800E+02 7.385E-11 0.000000 -63.759 -243.699
9 5.400E+02 9.385E-07 0.000008 89.991 -89.949

total harmonic distortion = 58.961298 percent

Как предсказывалось ранее, напряжение фазы нагрузки представляет собой почти чистую синусоиду с незначительным содержанием гармоник благодаря прямому соединению с фазами источника в системе Δ-Δ.

Но что случилось с тройными гармониками? Часто́ты 3-й и 9-й гармоник не проявляются в значительном количестве ни в линейном токе, ни в фазном напряжении нагрузки, ни в фазном токе источника! Мы знаем, что тройные (гармонические) токи должны быть, потому что источники тока 3-й и 9-й гармоник намеренно размещены в фазах нагрузки, но куда эти токи ушли?

Анализ влияния тройных гармоник в схеме Δ-Δ

Помните, что тройные гармоники основных частот, сдвинутых по фазе на 120°, находятся в фазе друг с другом.

Обратите внимание на направления, в которых указывают стрелки источников тока в фазах нагрузки, и подумайте, что произошло бы, если бы источники 3-й и 9-й гармоник были источниками постоянного тока.

То, что у нас было бы, сейчас циркулирует в контуре, образованном Δ-соединёнными фазами. Вот туда и ушли тройные гармонические токи: они остаются в пределах Δ-нагрузки, никогда не доходя до линейных проводников или обмоток источника.

Это можно изобразить графически:

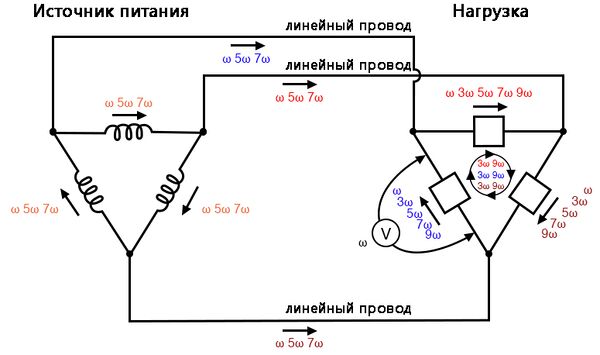
Рис. 22. Источник/нагрузка в Δ-Δ-схеме: фазы нагрузки получают неискаженные синусоидальные напряжения. Тройные гармонические токи циркулируют только в фазах нагрузки. Возникающие в линейных проводниках и в обмотках фаз источника питания токи не являются тройными гармоническими.

Это главное преимущество конфигурации системы Δ-Δ: тройные гармонические токи остаются ограниченными в любом наборе компонентов, которые их создают, и не «распространяются» на другие части системы.

Итог

  • Нелинейные компоненты – это те, у которых несинусоидальная волна тока при возбуждении синусоидальным напряжением. Поскольку любое искажение изначально чистой синусоидальной волны составляет гармонические частоты, можно утверждать, что нелинейные компоненты генерируют гармонические токи.
  • Когда синусоидальные искажения симметричны выше и ниже относительно средней центральной линии волны, гармоники будут иметь только нечётные, а не чётные номера.
  • Третья гармоника и ее целые кратные (6-я, 9-я, 12-я, 15-я) известны как тройные гармоники. Они находятся в фазе друг с другом, несмотря на то, что их соответствующие основные сигналы сдвинуты по фазе на 120° друг с другом.
  • В 4-проводной YY-системе в нейтральном проводе возникают тройные гармонические токи.
  • Тройные гармонические токи в Δ-связном наборе компонентов циркулируют в контуре, образованном Δ.

См.также

Внешние ссылки

  1. ↑ www.allaboutcircuits.com - Harmonics in Polyphase Power Systems
Партнерские ресурсы
Криптовалюты
Магазины
Хостинг
Разное
Теория по электронике
Постоянный ток
Основные концепты электричества • Статическое электричество • Проводники, диэлектрики и поток электронов • Что такое электрические цепи • Напряжение и электроток • Сопротивление • Напряжение и электроток в реальной цепи • Условный ток и поток электронов
Закон Ома • Закон Ома – Как напряжение, сила тока и сопротивление связаны друг с другом • Аналогия для закона Ома • Мощность в электрических цепях • Расчёт электрической мощности • Резисторы • Нелинейная проводимость • Построение цепи • Полярность перепада напряжения • Компьютерная симуляция электрических цепей
Правила электробезопасности • Важность правил электробезопасности • Воздействие электричества на психологическое состояние • Путь, который ток проходит перед ударом • Закон Ома (снова!) • Техника безопасности • Первая медицинская помощь при ударе током • Распространённые источники опасности • Проектирование электроцепей с учётом требований безопасности • Безопасное использование приборов для измерения электрических показателей • Данные о влиянии удара током на тело человека
Экспоненциальная запись и метрические приставки • Экспоненциальная запись • Арифметические операции для экспоненциальной записи • Метрические обозначения • Преобразование метрических приставок • Используем ручной калькулятор • Экспоненциальная форма в программе SPICE
Последовательные и параллельные электрические цепи • Что такое «последовательные» и «параллельные» электрические цепи • Простая последовательная цепь • Простая параллельная цепь • Электропроводность • Рассчитываем мощность • Правильно используем закон Ома • Анализ отказов компонентов цепи • Строим простые резистивные цепи
Схемы с делителями напряжения и правила Кирхгофа • Схемы с делителем напряжения • Правило напряжений Кирхгофа (ПНК) • Цепи – делители тока и формула делителя тока • Правило Кирхгофа для силы тока (ПКТ)
Комбинированные последовательно-параллельные схемы • Что такое последовательно-параллельная цепь • Методы анализа последовательно-параллельных резисторных цепей • Перерисовываем избыточно усложнённые схемы • Анализ отказов компонентов (продолжение) • Построение простых резисторных цепей
Измерения в электрических цепях постоянного тока • Что такое измеритель? • Как устроен вольтметр • Как вольтметр влияет на измеряемую цепь • Как устроен амперметр • Как амперметр влияет на измеряемую цепь • Как устроен омметр • Высоковольтный омметр • Мультиметры • Кельвиновское 4-проводное измерение сопротивления • Мостовые схемы • Как устроен ваттметр • Как самостоятельно сделать ручной калибратор
Сигналы электрического оборудования • Аналоговые и цифровые сигналы • Системы сигналов напряжения • Системы сигналов силы тока • Тахогенераторы • Теромопары • Измерения pH • Тензодатчики
Анализ сети постоянного тока • Что такое сетевой анализ? • Метод токов ветвей • Аналитический метод контурных токов • Метод узловых потенциалов • Введение в сетевые теоремы • Теорема Миллмана • Теорема о суперпозиции • Теорема Тевенена • Теорема Нортона • Эквивалентность схем Тевенена и Нортона • И вновь о теореме Миллмана • Теорема о передаче максимальной мощности • Δ-Y и Y-Δ преобразования
Батареи и системы питания • Поведение электронов при химических реакциях • Батарейные конструкции • Рейтинг батарей • Батареи специального назначения • Практические рекомендации при использовании батарей
Физика проводников и диэлектриков • Введение в физику проводников и диэлектриков • Размеры проводов• Допустимые токовые нагрузки на провода • Предохранители • Удельное сопротивление • Температурный коэффициент сопротивления • Сверхпроводимость • Пробивное напряжение диэлектрика
Конденсаторы • Электрическое поле и ёмкость • Конденсаторы и дифференциальное исчисление • Факторы, влияющие на ёмкость конденсатора • Последовательное и параллельное соединение конденсаторов • Практические соображения - Конденсаторы
Магнетизм и электромагнетизм • Постоянные магниты • Электромангетизм • Единицы измерения магнитных величин • Магнитная проницаемость и насыщение • Электромагнитная индукция • Взаимная индукция
Катушки индуктивности • Магнитные поля и индуктивность • Катушки индуктивности и дифференциальное исчисление • Факторы, влияющие на индуктивность • Катушки индуктивности в последовательных и параллельных соединениях • Практические соображения – Катушки индуктивности
Постоянные времени в RC и L/R цепях • Переходные процессы в электрических цепях • Переходные процессы в цепях с конденсатором • Переходные процессы в цепях с катушкой индуктивности • Расчёт напряжения и силы тока • Почему L/R, а не LR? • Комплексные расчёты напряжения и тока • Сложные схемы • Расчёт неизвестного времени
Переменный ток
Основы теории переменного тока • Что такое переменный ток? • Формы волн переменного тока • Измерение величин переменного тока • Расчёт простейшей цепи переменного тока • Фаза переменного тока • Принципы радио
Комплексные числа • Введение в комплексные числа • Векторы и волны переменного тока • Сложение простых векторов • Сложение сложных векторов • Полярная и алгебраическая запись комплексных чисел • Арифметика комплексных чисел • И ещё по поводу полярности переменного тока • Несколько примеров с цепями переменного тока
Реактанс и импеданс – Индуктивность • Резистор в цепи переменного тока (Индуктивность) • Катушка индуктивности в цепи переменного тока • Последовательные резистивно-индуктивные цепи • Параллельные резистивно-индуктивные цепи • Особенности катушек индуктивности • Что такое «скин-эффект»?
Реактанс и импеданс – Ёмкость • Резистор в цепи переменного тока (Ёмкость) • Конденсатор в цепи переменного тока • Последовательные резистивно-ёмкостные цепи • Параллельные резистивно-ёмкостные цепи • Особенности конденсаторов
Реактанс и импеданс – R/L/C-цепи • Обзор R, X и Z (сопротивление, реактанс и импеданс) • Последовательные R/L/C-цепи • Параллельные R/L/C-цепи • Последовательно-параллельные R/L/C-цепи • Реактивная проводимость и адмиттанс • R/L/C-цепи – что в итоге?
Резонанс • Электрический маятник • Простой параллельный резонанс (колебательный контур) • Простой последовательный резонанс • Применение резонанса • Резонанс в последовательно-параллельных цепях • Добротность и полоса пропускания резонансной цепи
Сигналы переменного тока смешанной частоты • Сигналы переменного тока смешанной частоты - Введение • Прямоугольные волновые сигналы • Другие волновые формы • Подробнее о спектральном анализе • Эффекты в электрических цепях
Фильтры • Что такое фильтр? • Низкочастотные фильтры • Высокочастотные фильтры • Полосовые фильтры • Полосно-заграждающие фильтры • Резонансные фильтры • Подводя итоги по фильтрам
Трансформаторы • Взаимная индуктивность и основные операции • Повышающие и понижающие трансформаторы • Электрическая изоляция • Фазировка • Конфигурации обмотки • Регулировка напряжения • Специальные трансформаторы и приложения • Практические соображения – Трансформаторы
Многофазные цепи переменного тока • Однофазные системы питания • Трёхфазные системы питания • Чередование фаз • Устройство многофазного двигателя • Трёхфазные Y- и дельта-конфигурации • Трёхфазные цепи с трансформатором • Гармоники в многофазных энергосистемах • Гармонические фазовые последовательности
Коэффициент мощности • Мощность в резистивных и реактивных цепях переменного тока • Истинная, реактивная и полная мощность • Расчёт коэффициента мощности • Практическая коррекция коэффициента мощности
Измерение цепей переменного тока • Вольтметры и амперметры переменного тока • Измерение частоты и фазы • Измерение мощности • Измерение качества электроэнергии • Мостовые схемы переменного тока • Измерительные преобразователи переменного тока
Двигатели переменного тока • Введение в двигатели переменного тока • Синхронные двигатели • Синхронный конденсатор • Двигатель с магнитным сопротивлением • Шаговые двигатели • Бесщёточный двигатель постоянного тока • Многофазные асинхронные двигатели Теслы • Асинхронные двигатели с фазным ротором • Однофазные асинхронные двигатели • Прочие специализированные двигатели • Сельсин-двигатели (синхронизированные двигатели) • Коллекторные двигатели переменного тока
Линии передачи • Кабель на 50 Ом? • Электрические цепи и скорость света • Характеристический импеданс • Линии передачи конечной длины • «Длинные» и «короткие» линии передачи • Стоячие волны и резонанс • Преобразование импеданса • Волноводы
Полупроводники
Усилители и активные устройства • От электрики к электронике • Активные и пассивные устройства • Усилители • Коэффициент усиления • Децибелы • Абсолютные дБ-шкалы • Аттенюаторы
Теория твердотельных приборов • Введение в теорию твердотельных устройств • Квантовая физика • Валентность и кристаллическая структура • Зонная теория твёрдых тел • Электроны и «дырки» • P-N-переход • Полупроводниковые диоды • Транзисторы с биполярным переходом • Полевые транзисторы • Полевые транзисторы с изолированным затвором (MOSFET) • Тиристоры • Методы производства полупроводников • Сверхпроводящие устройства • Квантовые устройства • Полупроводниковые приборы в SPICE
Диоды и выпрямители • Диоды и выпрямители – Введение • Проверка диодов мультиметром • Номинальные характеристики диодов • Схемы выпрямителей • Пиковый детектор • Схемы ограничителей напряжения • Схемы фиксаторов уровня • Умножители напряжения (удвоители, утроители, учетверители и т.д.) • Схемы коммутации индуктивных нагрузок • Диодные схемы коммутации • Что такое диод Зенера (стабилитрон)? • Диоды специального назначения • Прочие диодные технологии • Модели диодов в SPICE
Биполярные транзисторы • Транзисторы с биполярным переходом (ТБП) – Введение • Транзистор с биполярным переходом (ТБП) как переключатель • Проверка транзистора с биполярным переходом (ТБП) с помощью мультиметра • Активный режим работы транзистора с биполярным переходом (ТБП) • Усилительный каскад с общим эмиттером • Усилительный каскад с общим коллектором • Усилительный каскад с общей базой • Каскодный усилитель • Методы смещения для транзисторов с биполярным переходом (ТБП) • Расчёт смещения для транзисторов с биполярным переходом (ТБП) • Взаимодействие входа и выхода в транзисторах с биполярным переходом (ТБП) • Обратная связь в транзисторах с биполярным переходом (ТБП) • Импеданс усилителя • Токовые зеркала в транзисторах с биполярным переходом (ТБП) • Параметры и корпуса транзисторов с биполярным переходом (ТБП) • Особенности транзисторов с биполярным переходом (ТБП)
Полевые транзисторы • Полевые транзисторы (JFET) – Введение • Полевой транзистор (JFET) как переключатель • Проверка полевого транзистора (JFET) с помощью мультиметра • Активный режим работы полевого транзистора (JFET)
Полевые транзисторы с изолированным затвором • Полевые транзисторы с изолированным затвором – Введение • Обедняющие полевые транзисторы с изолированным затвором • Биполярные транзисторы с изолированным затвором
Тиристоры • Гистерезис • Газоразрядные лампы • Диод Шокли (динистор) • DIAC (симметричный динистор) • Управляемый кремниевый выпрямитель (SCR-тиристор) • TRIAC (симметричный тринистор, триак) • Оптотиристоры • Однопереходной транзистор • Управляемый кремниевый коммутатор (SCS-тиристор) • Тиристоры с полевым управлением
Операционные усилители • Операционные усилители (ОУ) – Введение • Несимметричные и дифференциальные усилители • «Операционный» усилитель • Отрицательная обратная связь • Делитель напряжения в цепи обратной связи • Аналогия для делителя напряжения в цепи обратной связи • Преобразование сигнала напряжения в сигнал тока • Схемы усреднителя и сумматора • Построение дифференциальных усилителей • Инструментальный (измерительный) усилитель • Схемы дифференциатора и интегратора • Положительная обратная связь • Практические аспекты ОУ • Модели операционных усилителей
Практические аналоговые полупроводниковые схемы • Электростатический разряд • Схемы источников питания • Схемы усилителей • Осцилляторные схемы • Радиосхемы • Вычислительные схемы • Измерительные схемы
Приводы двигателей постоянного тока • Широтно-импульсная модуляция
Электронные лампы • Электронные лампы – Введение • История электронных ламп – с чего всё началось • Триод • Тетрод • Силовой лучевой тетрод • Пентод • Комбинированные электронные лампы • Характеристики электронных ламп • Ионизированные (газовые) электронные лампы • Индикаторные электронные лампы • Микроволновые электронные лампы • Сравниваем электронные лампы и полупроводники
Цифровая электроника
Системы счисления • Числа и способы их выражения • Системы счисления • Сравниваем десятеричные и двоичные числа • Восьмеричная и шестнадцатеричная системы счисления • Восьмеричные и шестнадцатеричные числа преобразовываем в десятеричные • Преобразование из десятеричной системы счисления
Двоичная арифметика • Числа и системы счисления • Двоичное сложение • Отрицательные двоичные числа • Двоичное вычитание • Двоичное переполнение • Наборы битов
Логические вентили • Цифровые сигналы и вентили • Вентили «НЕ» • «Буферные» вентили • Вентили с более чем одним входом • Транзисторно-транзисторная логика вентилей «И-НЕ» и «И» • Транзисторно-транзисторная логика вентилей «ИЛИ-НЕ» и «ИЛИ» • Схемы КМОП-вентилей • Специальные выходы в вентилях • Универсальность вентилей «И-НЕ» и «ИЛИ-НЕ» • Уровни напряжения для «высоких» и «низких» логических сигналов • Вентильные DIP корпусы
Переключатели • Типы переключателей • Как устроены контакты переключателей • «Нормальное» состояние контакта и последовательное замыкание/размыкание • «Дребезжание» контактов
Электромеханические реле • Устройство реле • Контакторы • Реле с задержкой времени • Защитные реле • Твердотельные реле
Релейная логика • «Лестничные» диаграммы • Функции цифровой логики • Разрешающие и блокирующие схемы • Схемы управления двигателем • Отказоустойчивость • Программируемые логические контроллеры (ПЛК)
Булева алгебра • Булева алгебра – Введение • Логическая арифметика • Булевы алгебраические тождества • Булевы алгебраические свойства • Логические правила для упрощения • Примеры упрощения схем • Функция «Исключающее ИЛИ»: вентиль XOR • Законы де Моргана • Преобразование таблиц истинности в логические выражения
Карты Карно • Карты Карно – Введение • Диаграммы Венна и множества • Булевы соотношения на диаграммах Венна • Преобразование диаграмм Венна в карты Карно • Карты Карно, таблицы истинности и логические выражения • Упрощение логики с помощью карт Карно • Бо́льшие карты Карно с 4-мя переменными • Минтермы и макстермы в реализациях • Обозначения сумм и произведений • Поля «безразличия» на картах Карно • Бо́льшие карты Карно с 5-ю и 6-ю переменными
Функции комбинационной логики • Функции комбинационной логики – Введение • Неполный сумматор • Полный сумматор • Декодер • Кодер • Демультиплексоры • Мультиплексоры • Совместное использование множественных комбинационных схем
Мультивибраторы • Цифровая логика с обратной связью • SR-защёлка • Вентильная SR-защёлка • D-защёлка • Защёлки с запуском по фронту сигнала: триггеры • JK-триггер • Триггеры с асинхронными входами • Моностабильные мультивибраторы
Схемы последовательностей • Двоичная счётная последовательность • Асинхронные счётчики • Синхронные счётчики • Конечные автоматы
Сдвиговые регистры • Сдвиговые регистры – Введение • Сдвиговые регистры: последовательный вход, последовательный выход (SISO) • Сдвиговые регистры: параллельный вход, последовательный выход (PISO) • Сдвиговые регистры: последовательный вход, параллельный выход (SIPO) • Универсальные сдвиговые регистры: параллельный вход, параллельный выход (PIPO) • Кольцевые счётчики
Цифро-аналоговые и аналого-цифровые преобразования • Цифро-аналоговые (ЦАП) и аналого-цифровые (АЦП) преобразования – Введение • ЦАП R/2nR: цифро-аналоговый преобразователь с двоично-взвешенным входом • ЦАП R/2R: (цифро-аналоговый преобразователь) • Параллельные АЦП • Цифровые ступенчатые АЦП • АЦП с последовательным приближением • Отслеживающий АЦП • Скатные (интегрирующие) АЦП • Дельта-сигма АЦП • Практические аспекты схем АЦП
Цифровая связь • Цифровая связь – Введение • Сети и шины • Потоки данных • Типы электрических сигналов • Оптическая передача данных • Топология сети • Сетевые протоколы • Практические аспекты цифровой связи
Цифровое хранилище (память) • Почему «цифровое»? • Понятия и концепции цифровой памяти • Современная немеханическая память • Устаревшие немеханические технологии памяти • Постоянное запоминающее устройство (ПЗУ) • Память с движущимися частями: «Приводы»
Принципы цифровых вычислений • Двоичный сумматор • Таблицы поиска • Конечные автоматы • Микропроцессоры • Микропроцессорное программирование
Справочные материалы
Полезные уравнения и коэффициенты пересчёта • Уравнения и законы для цепей постоянного тока • Правила последовательных цепей • Правила параллельных цепей • Эквивалентные значения компонентов в последовательных и параллельных цепях • Уравнение ёмкости конденсатора • Уравнение катушки индуктивности • Уравнения постоянной времени • Уравнения цепей переменного тока • Уравнения для децибел • Метрические приставки и преобразования единиц измерения
Цветовая маркировка • Цветовая маркировка резисторов • Цветовая маркировка проводки • Инфографика цветовой маркировки проводки
Таблицы проводников и диэлектриков • Таблица калибров медной проволоки • Таблица допустимых нагрузок для медного провода • Коэффициенты удельного сопротивления • Таблица температурных коэффициентов сопротивления • Критические температуры для сверхпроводников • Диэлектрическая прочность изоляторов
Справочник по алгебре • Основные алгебраические тождества • Основные свойства арифметики • Свойства степеней • Извлечение корней • Важные константы • Логарифмы • Формулы сокращённого умножения • Квадратное уравнение • Прогрессии • Факториалы • Решение систем уравнений: метод подстановки и метод сложения
Справочник по тригонометрии • Тригонометрия прямоугольного треугольника • Тригонометрия произвольного треугольника • Тригонометрические формулы • Гиперболические функции
Справочник по исчислению • Формулы вычисления пределов • Производная числа • Общие производные • Производные показательных функций с основанием e • Производные простых тригонометрических функций • Правила вычисления производных • Первообразная (неопределённый интеграл) • Общие первообразные • Первообразные показательных функций от числа e • Правила вычисления первообразных • Определённые интегралы и основная теорема исчисления • Дифференциальные уравнения
Использование программы SPICE для моделирования электрических схем • Программа моделирования электрических цепей SPICE — Введение • История программы SPICE • Основы программирования в SPICE • Интерфейс командной строки • Компоненты электрических схем • Опции для проведения анализа • Странные особенности программы SPICE • Примеры электрических цепей и списков связей
Устранение неполадок – теория и практика • Вопросы, которые следует задать, прежде чем продолжить • Общие советы по устранению неполадок • Конкретные методы устранения неполадок • Вероятные сбои в проверенных системах • Вероятные сбои в непроверенных системах • Возможные ментальные ловушки
Схематические обозначения элементов цепи • Провода и соединения • Источники питания • Типы резисторов • Типы конденсаторов • Катушки индуктивности • Взаимные катушки индуктивности • Переключатели с ручным управлением • Управляемые процессом переключатели • Переключатели с электрическим приводом (реле) • Соединители • Диоды • Биполярные транзисторы • Переходные транзисторы с полевым эффектом (JFET) • Транзисторы с полевым эффектом с изолированным затвором (IGFET или MOSFET) • Гибридные транзисторы • Тиристоры • Интегральные схемы • Электронные лампы
Периодическая таблица химических элементов • Таблица Менделеева
Эксперименты
Введение • Электроника как точная наука • Обустраиваем домашнюю лабораторию
Основные концепции и испытательное оборудование • Использование вольтметра • Использование омметра • Очень простая схема • Использование амперметра при измерении силы тока • Закон Ома • Нелинейное сопротивление • Рассеяние мощности • Цепь с переключателем • Эксперимент по электромагнетизму • Эксперимент с электромагнитной индукцией
Электрические цепи постоянного тока • Электрические цепи постоянного тока – Введение • Последовательные источники питания • Параллельные источники питания • Делитель напряжения • Делитель тока • Потенциометр как делитель напряжения • Потенциометр как реостат • Прецизионный потенциометр • Ограничение диапазона реостата • Термоэлектричество • Мультиметр своими руками • Чувствительный детектор напряжения • Потенциометрический вольтметр • 4-проводное измерение сопротивления • Простейший компьютер • Картошка-батарейка • Зарядка и разрядка конденсатора • Индикатор скорости изменения
Электрические цепи переменного тока • Электрические цепи переменного тока – Введение • Трансформатор – блок питания • Сборка трансформатора • Переменный индуктор • Чувствительный аудиодетектор • Обнаружение магнитных полей переменного тока • Обнаружение электрических полей переменного тока • Альтернатор – автомобильный генератор • Асинхронный двигатель • Асинхронный двигатель побольше • Фазовый сдвиг • Погашение звука • Музыкальный синтезатор как генератор сигналов • ПК-осциллограф • Анализ волновых сигналов • Колебательный контур • Сигнальная связь
Дискретные полупроводниковые схемы • Дискретные полупроводниковые схемы – Введение • Коммутирующий диод • Полупериодный выпрямитель • Двухполупериодный мостовой выпрямитель • Двухполупериодный выпрямитель с центральным отводом • Цепь «выпрямитель/фильтр» • Регулятор напряжения • Транзистор как переключатель • Датчик статического электричества • Датчик импульсного света • Повторитель напряжения • Усилитель с общим эмиттером • Многокаскадный усилитель • Как построить схему токового зеркала • JFET – регулятор тока • Дифференциальный усилитель • Простой операционный усилитель • Аудио осциллограф • Ламповый аудио усилитель
Аналоговые интегральные схемы • Аналоговые интегральные схемы – Введение • Компаратор напряжения • Прецизионный повторитель напряжения • Неинвертирующий усилитель • Высокоимпедансный вольтметр • Интегратор • Аудио осциллограф на таймерной схеме 555 • Наклонный генератор на таймерной схеме 555 • ШИМ-контроллер мощности • Аудиоусилитель класса B
Цифровые интегральные схемы • Цифровые интегральные схемы – Введение • Основная функция вентилей • SR-защёлка на основе вентилей «ИЛИ-НЕ» • SR-защёлка на основе вентиля «И-НЕ» с входом разрешения • SR-триггер на основе вентиля «И-НЕ» • Светодиодный секвенсор • Простейший кодовый замок • 3-битный двоичный счётчик • 7-сегментный дисплей
Таймерные схемы 555 • Интегральный таймер 555 • Триггер Шмитта на интегральном таймере 555 • Гистерезисный осциллограф на интегральном таймере 555 • Моностабильный мультивибратор на интегральном таймере 555 • Минимальное количество комплектующих для КМОП-схемы 555 проблескового прибора длительного действия на красных светодиодах • КМОП-схема 555 проблескового прибора длительного действия на синих светодиодах • КМОП-схема 555 проблескового прибора длительного действия на светодиодах обратного хода • КМОП-схема 555 проблескового прибора длительного действия на красных светодиодах

Источник — http://wikihandbk.com/ruwiki/index.php?title=Электроника:Переменный_ток/Многофазные_цепи_переменного_тока/Гармоники_в_многофазных_энергосистемах&oldid=7737412