Электроника:Постоянный ток/Анализ сети постоянного тока/Δ-Y и Y-Δ преобразования

Содержание

Теория

Практика

Проверка знаний

Рецепты

Эксперименты

Резерв

Резерв

Резерв

Резерв

Перевод: Макаров В. (valemak)

Проверка/Оформление/Редактирование: Мякишев Е.А.

Δ-Y и Y-Δ преобразования

Во многих схемах встречаются компоненты, соединенные вместе одним из двух способов, которыми можно сформировать трехконтактную сеть: конфигурация «дельта» или Δ (также известная как «Пи» или «π»). А также конфигурация «Y» (также известная как «T» или «звезда»).

Рис. 1. Схема сети с тремя терминалами. Слева в двух эквивалентных вариантах – Δ (другие названия – «дельта», «треугольник», «пи», «π»). Справа в двух эквивалентных вариантах – Y (другие названия – «Т», «звезда», «тройник»).

Можно рассчитать правильные значения резисторов, необходимых для формирования одного типа сети (Δ или Y), который ведёт себя идентично другому типу, если анализировать только на основе клеммных соединений. То есть, если бы у нас были две отдельные цепи резисторов, одна Δ и одна Y, каждая со своими резисторами, скрытыми из поля зрения, и только три клеммы (A, B и C), которые открыты для тестирования, замеры показали бы, что резисторы могут относиться как к одному типу, так и к другому. И нет возможности электрически определить, какой именно тип сети использован. Другими словами, эквивалентные сети Δ и Y ведут себя одинаково.

Уравнения преобразования Δ и Y

Для преобразования одной сети в другую используется несколько уравнений:

Рис. 2. Уравнения преобразования «дельта-звезда».

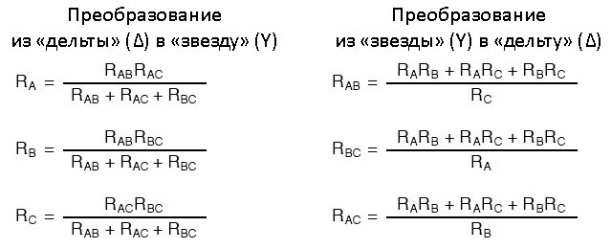
Сети Δ и Y часто встречаются в трёхфазных энергосистемах переменного тока (эта тема рассматривается в томе II этой серии книг), но даже в этом случае они обычно являются сбалансированными сетями (все резисторы имеют равные номиналы) и преобразование одной сети в другую не требует сложных вычислений. В каких случаях среднему специалисту это может понадобиться?

Применение преобразования Δ-Y

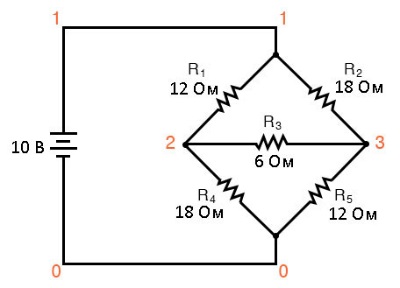
Основное применение для преобразования Δ-Y – решение несбалансированных мостовых схем, наподобие такой:

Рис. 3. Преобразования Δ-Y применяются для анализа несбалансированных мостовых схем.

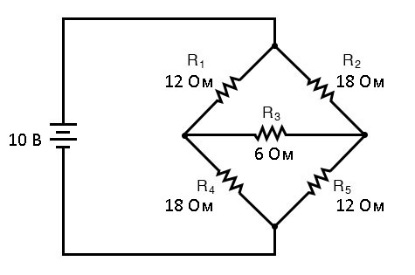
Решить эту схемы аналитическим методом токов ветвей или методом контурных токов можно, но сложно. Теорема Миллмана или теорема суперпозиции тут вообще неприменимы, поскольку в схеме только один источник питания.

Можно ещё, конечно, попробовать теорему Тевенина или Нортона, рассматривая R₃ как нагрузку, но, думаете, это будет очень смешно?

Если бы мы рассматривали резисторы R₁, R₂ и R₃ как подключенные по схеме Δ (переобозначим их как R_ab, R_ac и R_bc соответственно, чтобы подчеркнуть, что эти резисторы находятся на трёх проводах, соединяющих три точки A, B и С) и заменили бы их на эквивалентную Y-конфигурацию, мы могли бы преобразовать этот мост в более простую последовательно-параллельную схему:

Рис. 4. Выбираем участок, по конфигурации являющийся дельта-сетью, чтобы преобразовать этот кусок схемы в Y-сеть. Отметим, что это преобразование чаще всего является виртуальным, это не означает что на физическом уровне что-либо меняется (хотя, при желании можно и переподключить провода в другой конфигурации и выбрать другие резисторы с соответствующими сопротивлениями, в результате чего получим эквивалентную мостовую схему). На практике, элементы так и остаются, например, в конфигурации «дельта», но в согласии с уравнениями перехода, анализировать их будем так, будто они расположены в виде «звезды» (при этом не стоит забывать, что у виртуальных резисторов, в соответствии с уравнениями будут другие значения сопротивлений). Так как обе конфигурации электрически эквивалентны, на итоговом результате это не отразится.

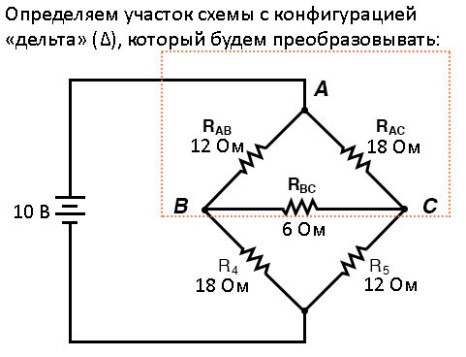
Итак, производим Δ-Y-преобразование…

Рис. 5. Участок схемы с конфигурацией «дельта» преобразовали в участок с конфигурацией «звезда».

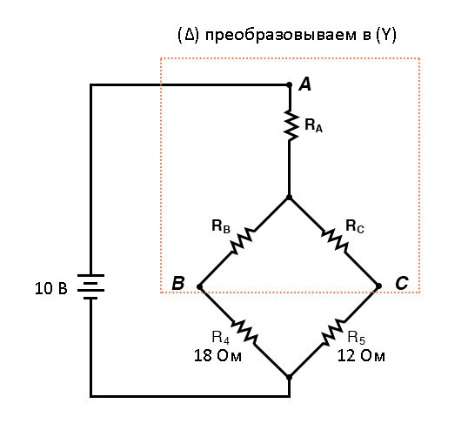
Если мы выполним наши расчёты правильно, напряжения между точками A, B и C в преобразованной схеме будут такими же, как и в исходной схеме, и мы сможем перенести эти значения обратно в исходную конфигурацию моста.

Рис. 6. Вычисляем сопротивления для резисторов новой конфигурации.

Рис. 7. На преобразованной схеме отметим новые значения сопротивлений резисторов.

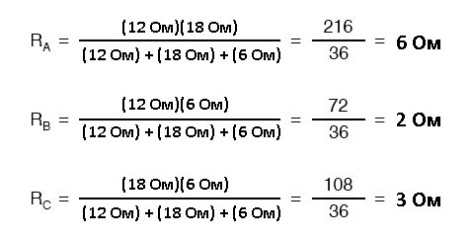
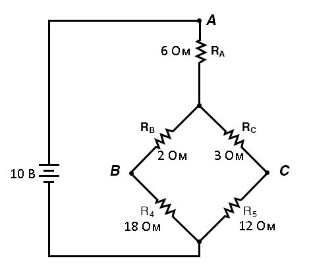
Резисторы R₄ и R₅, естественно, остаются прежними на 18 Ом и 12 Ом соответственно. Анализируя схему как последовательно-параллельную, приходим к следующим цифрам:

Рис. 8. Табличным методом рассчитываем напряжения и силы тока, проходящие через элементы нашей преобразованной схемы (которая теперь классифицируется как последовательно-параллельная).

Мы должны использовать значения падения напряжения из таблицы выше, чтобы определить напряжения между точками A, B и C, складывая или вычитая (зависит от того совпадает направление полярностей или нет, как в случае с напряжением между точками B и C):

Рис. 9. Определяем напряжения между точками A, B и C. Направления полярностей у пар R_A/R_B и R_A/R_C совпадает, поэтому эти напряжения складываем, получая напряжение на участке между точками. Направления полярностей у пары R_B/R_C взаимно противоположны, чтобы получить напряжение между точками B и C, вычитаем напряжения у соответствующих резисторов.

Рис. 10. Найденные напряжения между точками A, B и C (вольты перевели в милливольты).

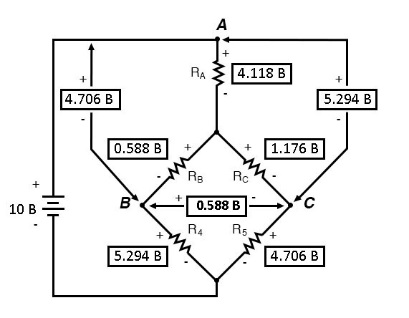
Теперь, когда мы знаем эти напряжения, мы можем передать их в те же точки A, B и C в исходной мостовой схеме:

Рис. 11. Возвращаемся к изначальной мостовой схеме. Но теперь нам известны напряжения на участках с резисторами.

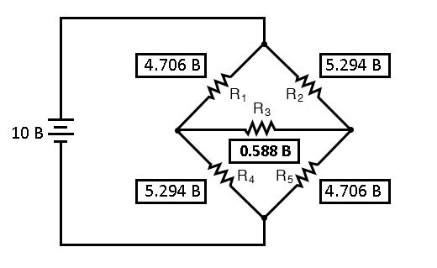
Падения напряжения на R₄ и R₅, естественно, точно такие же, как и в цепи, где «дельта» была преобразована в «звезду».

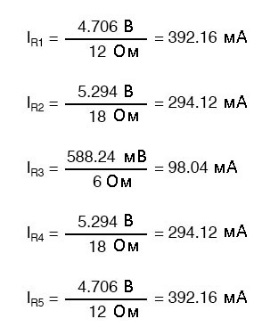
На этом этапе мы могли бы взять эти напряжения и определить силы токи резисторов с помощью многократного использования закона Ома (I = E/R):

Рис. 12. Вычислив напряжения, теперь с помощью закона Ома определяем силы тока, проходящий через резисторы.

Моделирование с использованием SPICE

Проверим наши расчёты с помощью быстрой симуляции в SPICE:

Рис. 13. Проверяемая несбалансированная мостовая схема. Отмечены узлы, между которыми находятся элементы цепи.

unbalanced bridge circuit  
v1 1 0 
R1 1 2 12      
R2 1 3 18      
R3 2 3 6
R4 2 0 18      
R5 3 0 12      
.dc v1 10 10 1 
.print dc v(1,2) v(1,3) v(2,3) v(2,0) v(3,0)   
.end
v1            v(1,2) v(1,3)         v(2,3)      v(2)         v(3)           
1.000E+01     4.706E+00 5.294E+00   5.882E-01   5.294E+00    4.706E+00

Итоговые числа на последней строке, перечисленные слева направо, обозначают падения напряжения на пяти соответствующих резисторах с R₁ по R₅. Я мог бы также показать силы тока, но это потребовало бы вставки «фиктивных» источников напряжения в список соединений SPICE. А поскольку нас в первую очередь интересует проверка уравнений Δ-Y-преобразования, а не закона Ома, то уже сделанного будет вполне достаточно.

Итог

• Сети Δ-конфигурации также известны как сети типа «дельта», «Пи», «π».
• Сети Y-конфигурации также известны как сети типа «звезда» или «T».
• Сети Δ и Y могут быть преобразованы в их эквивалентные аналоги с помощью соответствующих уравнений сопротивления. Под «эквивалентностью» подразумевается, что две сети будут электрически идентичны, если измерять их от трёх клемм (A, B и C).
• Мостовую схему можно упростить до последовательно-параллельной схемы, преобразовав часть цепи из Δ-конфигурации в Y-конфигрурацию. В результате устраняется падение напряжения между исходными тремя точками подключения (A, B и C), что позволяет передать эти напряжения обратно в исходную мостовую схему через те же самые эквивалентные точки.