Электроника:Постоянный ток/Анализ сети постоянного тока/Метод узловых потенциалов

Содержание

Теория

Практика

Проверка знаний

Рецепты

Эксперименты

Резерв

Резерв

Резерв

Резерв

Перевод: Макаров В. (valemak)

Проверка/Оформление/Редактирование: Мякишев Е.А.

Метод узловых потенциалов

Аналитический метод узловых потенциалов находит неизвестные напряжения в узлах схемы с помощью системы уравнений ПКТ (правило Кирхгофа для силы тока). Такой подход выглядит необычным, поскольку он предполагает замену источников напряжения эквивалентными источниками тока. Более того, значения сопротивлений в омах заменяются на эквивалентную электрическую проводимость (электропроводность или просто проводимость) измеряемую в сименсах, G = 1/R. Сименс (См, англ. S) – это единица электрической проводимости, заменившая устаревшую единицу измерения мо (англ. mho). В любом случае, См = Ом^-1. И См показывает то же самое, что и устаревшее мо.

Метод расчёта узловых потенциалов

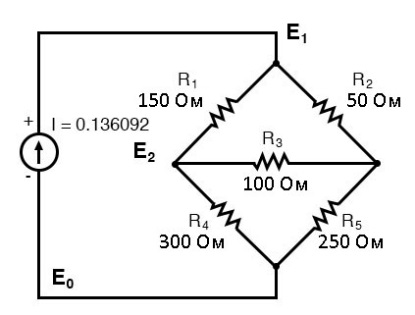
Начнем со схемы, на которой изображены обычные источники напряжения. Выберем общий узел Е₀ в качестве опорной точки. Узловые напряжения E₁ и E₂ вычисляются относительно этой точки.

Рис. 1. Схема с обычными источниками напряжения.

Рис. 2. Такой будет замена узлов на схеме, вместо источников напряжения теперь источники тока. Последовательные (по отношению к источнику напряжения) резисторы становятся параллельными (по отношению к источнику тока). Величина силы тока подбирается таким образом, чтобы в ветви создавалось эквивалентное напряжение.

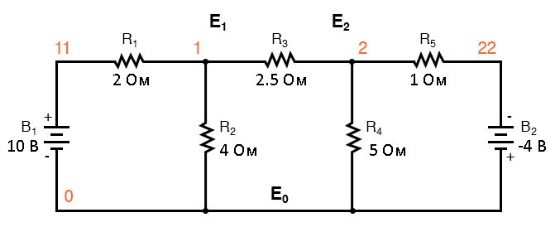
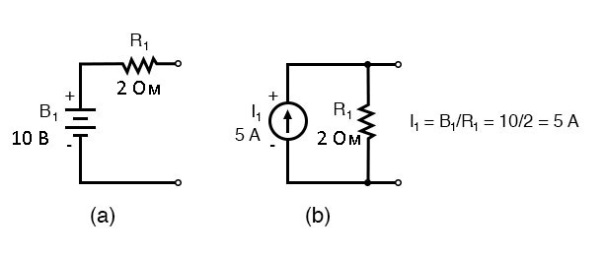
Замена источников напряжения и связанных последовательных резисторов эквивалентными источниками тока и параллельными резисторами приводит к изменениям в схеме. Заменяем сопротивление в омах электрической проводимостью в сименсах.

I1 = E1/R1 = 10/2 = 5 A
I2 = E2/R5 = 4/1 = 4 A
G1 = 1/R1 = 1/2 Ω   = 0.5 S
G2 = 1/R2 = 1/4 Ω   = 0.25 S
G3 = 1/R3 = 1/2.5 Ω = 0.4 S
G4 = 1/R4 = 1/5 Ω   = 0.2 S
G5 = 1/R5 = 1/1 Ω   = 1.0 S

Рис. 3. Вместо источников напряжения – источники тока (сила тока такова, чтобы создавалось эквивалентное напряжение). Вместо последовательных резисторов – параллельные. Вместо сопротивления - электрическая проводимость.

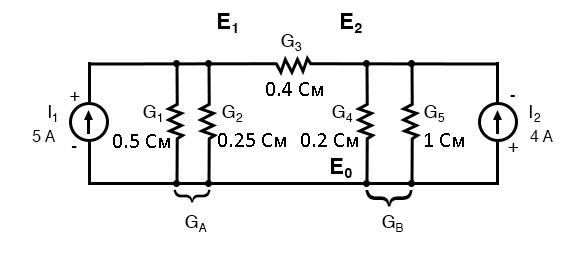
Можно ещё упростить, объединив параллельные проводимости (бывшие сопротивления). Но перерисовывать схему не будем. Она уже и так готова к применению метода узлового напряжения.

GA = G1 + G2 = 0,5 S + 0,25 S = 0,75 S
GB = G4 + G5 = 0,2 S + 1 S = 1,2 S

Исходя из общих принципов метода узлового напряжения, мы составим пару уравнений ПКТ, подставив в них узловые напряжения V₁ и V₂. Мы делаем это, чтобы проиллюстрировать схему написания обходных уравнений.

GAE1 + G3 (E1 - E2) = I1 (1)
GBE2 - G3 (E1 - E2) = I2 (2)
(GA + G3) E1 -G3E2 = I1 (1)
-G3E1 + (GB + G3) E2 = I2 (2)

Коэффициенты последней пары уравнений выше перегруппированы, чтобы показать закономерность. Сумма проводимостей, подключённых к первому узлу, является положительным коэффициентом первого напряжения в уравнении (1). Сумма проводимостей, подключённых ко второму узлу, является положительным коэффициентом второго напряжения в уравнении (2). Остальные коэффициенты отрицательны и представляют собой проводимость между узлами.

Для обоих уравнений правая часть равна соответствующему источнику тока, подключённого к узлу. Этот шаблон позволяет нам быстро писать обходные уравнения. Это приводит к набору правил для аналитического метода узловых потенциалов.

Правила узловых потенциалов:

• Преобразуйте источник напряжения, включенный последовательно с резистором, в эквивалентный источник тока с параллельным резистором.
• Измените значения сопротивления на электропроводность.
• Выберите опорный узел (E₀).
• Обозначьте на остальных узлах неизвестные напряжения (E₁)(E₂)...(E_N).
• Напишите уравнение ПКТ для каждого узла 1, 2, ..., N. Положительный коэффициент первого напряжения в первом уравнении представляет собой сумму проводимостей, подключенных к узлу. Коэффициент для второго напряжения во втором уравнении – это сумма проводимостей, подключенных к этому узлу. Повторите это для коэффициента третьего напряжения в третьем уравнении и так далее и для остальных уравнений. Если уравнения написать по порядку одно под другим, то эти коэффициенты расположены как бы «по диагонали».
• Все остальные коэффициенты для всех уравнений отрицательны и представляют собой проводимости между узлами. Первое уравнение, второй коэффициент – это проводимость участка от узла 1 к узлу 2, третий коэффициент – это проводимость участка от узла 1 к узлу 3. Аналогично заполняются отрицательные коэффициенты для других уравнений.
• Правая часть уравнений – это источник тока, подключенный к соответствующим узлам.
• Решите систему уравнений для неизвестных напряжений в узлах.

Пример применения метода узловых потенциалов

Задание:

Составьте уравнения и решите для напряжений в узлах, используя числовые значения на рисунке выше.

Решение:

(0,5 + 0,25 + 0,4) E1 - (0,4) E2 = 5 
- (0,4) E1 + (0,4 + 0,2 + 1,0) E2 = -4
(1.15) E1 - (0.4) E2 = 5 
- (0,4) E1 + (1,6) E2 = -4
E1 = 3,8095
E2 = -1,5476

Решение этой системы из двух уравнений может быть выполнено с помощью калькулятора или программы Октава (этот вариант тут не показан). Решение проверено в SPICE на основе оригинальной принципиальной схемы с источниками напряжения. Хотя в SPICE можно смоделировать и схему с источниками тока.

V1 11 0 DC 10
V2 22 0 DC -4
r1 11 1 2
r2 1 0 4
r3 1 2 2.5
r4 2 0 5
r5 2 22 1
.DC V1 10 10 1 V2 -4 -4 1 
.print DC V(1) V(2)
.end

v(1)            v(2)
3.809524e+00    -1.547619e+00

Посмотрим ещё один пример. Здесь три узла. На принципиальной схеме проводимость не указываем. Однако она просто вычисляется: G₁ = 1/R₁, G₂ = 1/R₂ и т.д.

Рис. 4. Схема из прошлой лекции с несбалансированным мостом Витстона. Вместо источника напряжения – источник тока.

Есть три узла, для которых можно написать обходные уравнения. Обратите внимание, что для уравнения (1) положителен коэффициент у E₁, для уравнения (2) положителен коэффициент у E₂ и для уравнения (3) положителен коэффициент у E₃. Эти коэффициенты – суммы всех проводимостей, подключенных к этим узлам. Все остальные коэффициенты отрицательны, что соответствует проводимости между узлами. Правая часть уравнений – это связанный источник тока, 0,136092 А для единственного источника тока в узле 1. Остальные уравнения в правой части равны нулю из-за отсутствия источников тока. Нам лень рассчитывать проводимости резисторов на схеме. Таким образом, G в нижнем индексе – это коэффициенты.

(G1 + G2) E1 -G1E2 -G2E3 = 0,136092
-G1E1 + (G1 + G3 + G4) E2 -G3E3 = 0
-G2E1 -G3E2 + (G2 + G3 + G5) E3 = 0

Мы настолько ленивы, что вводим взаимные сопротивления и суммы взаимных сопротивлений в матрицу Октавы «А», позволяя Октаве вычислить матрицу проводимости после «А =». Первоначальная входящая строка была такой длинной, что её разбили на три ряда. Это отличается от предыдущих примеров. Введённая матрица «А» ограничена начальной и конечной квадратными скобками. Столбцы матрицы разделяются пробелами. Строки матрицы разделяются символом «перевод строки». Запятые и точки с запятой в качестве разделителей не нужны. Тем не менее, вектор тока в «b» разделён точкой с запятой, чтобы получить вектор-столбец токов.

octave:12> A = [1/150+1/50 -1/150 -1/50
           > -1/150 1/150+1/100+1/300 -1/100
           > -1/50 -1/100 1/50+1/100+1/250]
           A =
              0.0266667  -0.0066667  -0.0200000
             -0.0066667   0.0200000  -0.0100000
             -0.0200000  -0.0100000   0.0340000

           octave:13> b = [0.136092;0;0]
           b =
              0.13609
              0.00000
              0.00000

           octave:14> x=A\b
           x =
              24.000
              17.655
              19.310

Обратите внимание, что диагональные коэффициенты матрицы «A» положительны, а все остальные коэффициенты отрицательны.

Решение в виде вектора напряжения находится в точке «x». E₁ = 24,000 В, E₂ = 17,655 В, E₃ = 19,310 В. Эти три напряжения оказываются равными предыдущим значениям контурных токов (из прошлой лекции, где мы решили такой же мост другим методом) и с решениями SPICE для того несимметричного моста. Это не случайное совпадение, так как источник тока, равный 0,13609 А был специально подобран так, чтобы он оказался эквивалентным источнику напряжения 24 В, используемого в прошлый раз в такой же задаче.

Итог

• Для сети, состоящей из элементов с электропроводностью и источников тока, аналитический метод узловых потенциалов находит неизвестные напряжения в узлах с помощью уравнений ПКТ.
• Подробные рекомендации по составлению обходных уравнений – см. вышеприведённые в этой лекции правила.
• Единица проводимости G – сименс (S). Проводимость обратно пропорциональна сопротивлению: G = 1/R.