Электроника:Цифровая электроника/Карты Карно/Обозначения сумм и произведений
Обозначения сумм и произведений[1]
Для справки, в этом разделе вводится терминология, используемая в некоторых текстах для описания минтермов и макстермов, отображаемых на картах Карно. В остальном нового материала здесь нет.
Обозначения для минтермов
Σ (сигма) обозначает сумму, а строчная буква «m» обозначает минтермы. Σm обозначает сумму минтермов. К следующему примеру мы вернёмся, чтобы это проиллюстрировать. Вместо описания непростой логики посредством логического уравнения мы перечисляем минтермы:
| f(A, B, C, D) = Σm(0, 1, 3, 4, 5, 7, 12, 13, 15) или f(A, B, C, D) = Σ(m0, m1, m3, m4, m5, m7, m12, m13, m15) |
Цифры указывают на местоположение ячейки или адрес на карте Карно, как показано в правой части рисунка 1 ниже. Это, безусловно, компактное средство описания списка минтермов или ячеек на K-карте.
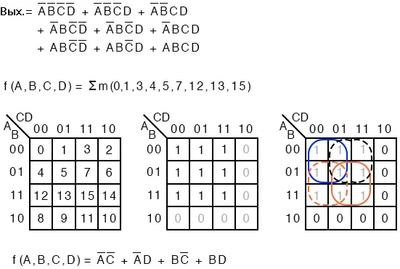
Новая терминология не влияет на решение Суммы-Произведений. Минтермы, в виде единиц на карте сгруппированы как обычно, и это способ записи решения для Суммы-Произведений.
Обозначения для макстермов
Ниже представлена терминология для описания списка макстермов. Произведение обозначается заглавной греческой буквой Π (пи), а заглавная буква «M» обозначает макстермы. ΠM обозначает произведение макстермов. Проиллюстрируем на том же примере.
Описание непростой логики булевым уравнением заменяется списком макстермов.
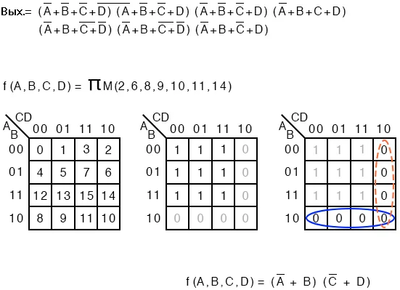
| f(A, B, C, D) = ΠM(2, 6, 8, 9, 10, 11, 14) или f(A, B, C, D) = Π(M2, M6, M8, M9, M10, M11, M14) |
И снова числа указывают на расположение адресов ячеек K-карты. Для макстермов это расположение нулей, как показано на рисунке 2 ниже. Решение для Произведения-Сумм производится обычным образом.
См.также
Внешние ссылки