Электроника:Постоянный ток/Экспоненциальная запись и метрические приставки/Метрические обозначения: различия между версиями

Материал из Онлайн справочника
Перейти к навигацииПерейти к поиску
Нет описания правки
Нет описания правки
 
(не показаны 4 промежуточные версии 1 участника)
Строка 1: Строка 1:
{{Блок/Панель навигации1
|заголовок=Экспоненциальная запись и метрические приставки
|назад=Электроника:Постоянный ток/Экспоненциальная запись и метрические приставки/Арифметические операции для экспоненциальной записи
|вперед=Электроника:Постоянный ток/Экспоненциальная запись и метрические приставки/Преобразование метрических приставок
}}
{{Панель управления/Электроника}}
{{Панель управления/Электроника}}
{{Перевод от valemak}}
{{Перевод от valemak}}
Строка 5: Строка 10:
=Метрические обозначения<ref>[https://www.allaboutcircuits.com/textbook/direct-current/chpt-4/metric-notation/ www.allaboutcircuits.com - Metric Notation Chapter 4 - Scientific Notation And Metric Prefixes]</ref>=
=Метрические обозначения<ref>[https://www.allaboutcircuits.com/textbook/direct-current/chpt-4/metric-notation/ www.allaboutcircuits.com - Metric Notation Chapter 4 - Scientific Notation And Metric Prefixes]</ref>=


Метрическая система представляет собой набор единиц измерения практически для любых физических величин, и кроме того, она выстроена на основе экспоненциальной записи. Главная особенность заключается в том, что степени десятки представлены с помощью специальных приставок в виде определённых букв алфавита, а не буквально в виде степеней десяток. В числовой шкале, приведённой ниже, показаны некоторые из наиболее употребляемых приставок и соответствующие им степени десятки:
[[Метрическая система]] представляет собой набор единиц измерения практически для любых физических величин, и кроме того, она выстроена на основе [[экспоненциальной записи]]. Главная особенность заключается в том, что степени десятки представлены с помощью специальных приставок в виде определённых букв алфавита, а не буквально в виде степеней десяток. В числовой шкале, приведённой ниже, показаны некоторые из наиболее употребляемых приставок и соответствующие им степени десятки:
   
   
[[File:metric-prefix-scale.png|center]]
[[File:metric-prefix-scale.png|center]]


Ориентируясь на данное масштабирование, видно, что, к примеру, 2,5 гигабайта будут означать 2,5 x 109 байт, или 2,5 миллиарда байтов. Точно также, 3,21 пА будут означать 3,21 × 10-12 ампер, или 3,21 триллионных ампер.
Ориентируясь на данное масштабирование, видно, что, к примеру, 2,5 гигабайта будут означать 2,5 x 10<sup>9</sup> байт, или 2,5 миллиарда байтов. Точно также, 3,21 пА будут означать 3,21 × 10<sup>-12</sup> ампер, или 3,21 триллионных ампер.


Есть и другие метрические приставки, соответствующие степеням десятки для крайне малых и крайне больших множителей. На крайне малой части спектра, фемто (ф) = 10-15, атто (а) = 10-18,  зепто (з) = 10-21 и иокто (и) = 10-24. На крайне большом конце спектра пета (П) = 1015, экса (Э) = 1018, зетта (З) = 1021 и иотта (И) = 1024.
Есть и другие метрические приставки, соответствующие степеням десятки для крайне малых и крайне больших множителей. На крайне малой части спектра, фемто (ф) = 10<sup>-15</sup>, атто (а) = 10<sup>-18</sup>,  зепто (з) = 10<sup>-21</sup> и иокто (и) = 10<sup>-24</sup>. На крайне большом конце спектра пета (П) = 10<sup>15</sup>, экса (Э) = 10<sup>18</sup>, зетта (З) = 10<sup>21</sup> и иотта (И) = 10<sup>24</sup>.


Так как основные приставки в метрической системе являются степенями десятки, кратными 3 (от «кило» и далее вверх и от «милли» и далее вниз), метрическая запись отличается от обычной экспоненциальной тем, что мантисса (т.е. набор значащих цифр) может быть в диапазоне от 1 до 999, в зависимости от того, какая приставка используется. Например, если лабораторный образец весит 0,000267 грамм, в экспоненциальной и метрической записях это будет выражаться по-разному:
Так как основные приставки в метрической системе являются степенями десятки, кратными 3 (от «кило» и далее вверх и от «милли» и далее вниз), метрическая запись отличается от обычной экспоненциальной тем, что мантисса (т.е. набор значащих цифр) может быть в диапазоне от 1 до 999, в зависимости от того, какая приставка используется. Например, если лабораторный образец весит 0,000267 грамм, в экспоненциальной и метрической записях это будет выражаться по-разному:


'''''2,67 x 10-4 грамм (в экспоненциальной форме)'''''
'''''2,67 x 10<sup>-4</sup> грамм (в экспоненциальной форме)'''''


'''''267 мкг (в метрической системе)'''''
'''''267 мкг (в метрической системе)'''''
{{ads2}}


Это же число также можно выразить как 0,267 миллиграмм (0,267 мг), хотя более распространённым подходом является представление набора значащих цифр в виде числа, больше единицы.
Это же число также можно выразить как 0,267 миллиграмм (0,267 мг), хотя более распространённым подходом является представление набора значащих цифр в виде числа, больше единицы.
Строка 29: Строка 36:
=См.также=
=См.также=


{{ads}}
 


=Внешние ссылки=
=Внешние ссылки=


<references />
<references />
{{Навигационная таблица/Электроника}}
{{Навигационная таблица/Портал/Электроника}}
{{Навигационная таблица/Телепорт}}
 
{{Блок/Панель навигации1
|заголовок=Экспоненциальная запись и метрические приставки
|назад=Электроника:Постоянный ток/Экспоненциальная запись и метрические приставки/Арифметические операции для экспоненциальной записи
|вперед=Электроника:Постоянный ток/Экспоненциальная запись и метрические приставки/Преобразование метрических приставок
}}
[[Категория:Постоянный ток]]
[[Категория:Постоянный ток]]
[[Категория:Метрические обозначения]]
[[Категория:Метрические обозначения]]
[[Категория:Экспоненциальная запись и метрические приставки]]
[[Категория:Экспоненциальная запись и метрические приставки]]
[[Категория:Метрические обозначения]]
[[Категория:Метрические обозначения]]
[[Категория:Теория]]
[[Категория:Теория по электронике]]

Текущая версия от 21:49, 22 мая 2023

←Экспоненциальная запись и метрические приставки→

Перевод: Макаров В. (valemak)
Проверка/Оформление/Редактирование: Мякишев Е.А.


Метрические обозначения[1]

Метрическая система представляет собой набор единиц измерения практически для любых физических величин, и кроме того, она выстроена на основе экспоненциальной записи. Главная особенность заключается в том, что степени десятки представлены с помощью специальных приставок в виде определённых букв алфавита, а не буквально в виде степеней десяток. В числовой шкале, приведённой ниже, показаны некоторые из наиболее употребляемых приставок и соответствующие им степени десятки:

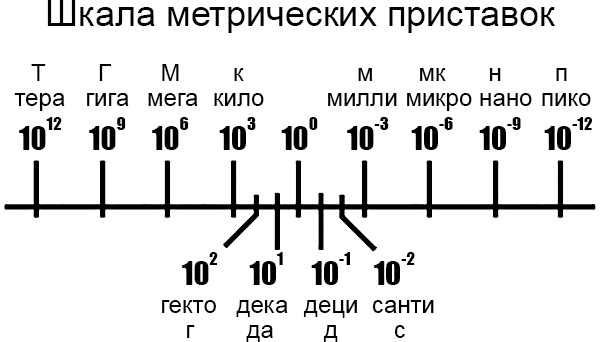
Ориентируясь на данное масштабирование, видно, что, к примеру, 2,5 гигабайта будут означать 2,5 x 109 байт, или 2,5 миллиарда байтов. Точно также, 3,21 пА будут означать 3,21 × 10-12 ампер, или 3,21 триллионных ампер.

Есть и другие метрические приставки, соответствующие степеням десятки для крайне малых и крайне больших множителей. На крайне малой части спектра, фемто (ф) = 10-15, атто (а) = 10-18, зепто (з) = 10-21 и иокто (и) = 10-24. На крайне большом конце спектра пета (П) = 1015, экса (Э) = 1018, зетта (З) = 1021 и иотта (И) = 1024.

Так как основные приставки в метрической системе являются степенями десятки, кратными 3 (от «кило» и далее вверх и от «милли» и далее вниз), метрическая запись отличается от обычной экспоненциальной тем, что мантисса (т.е. набор значащих цифр) может быть в диапазоне от 1 до 999, в зависимости от того, какая приставка используется. Например, если лабораторный образец весит 0,000267 грамм, в экспоненциальной и метрической записях это будет выражаться по-разному:

2,67 x 10-4 грамм (в экспоненциальной форме)

267 мкг (в метрической системе)

Это же число также можно выразить как 0,267 миллиграмм (0,267 мг), хотя более распространённым подходом является представление набора значащих цифр в виде числа, больше единицы.

В последнее время возник новый стиль метрической записи электрических величин, в котором избегается использование десятичного знака. Поскольку десятичные знаки (точка или запятая) часто неправильно интерпретируются и/или "теряются" ввиду низкого качества печати, такие величины, как 4,7 к, могут быть ошибочно восприняты как 47 к. В обновлённой нотации десятичный знак заменяется на символ метрической приставки, то есть «4,7 к» пишется как «4к7». Наше последнее число из предыдущего примера, «0,267 м», будет выражено в новых обозначениях как «0м267».

Итог

  • Система метрических обозначений использует буквенные приставки, соответствующие определённым степеням десятки вместо более длинной экспоненциальной записи.

См.также

Внешние ссылки

  1. ↑ www.allaboutcircuits.com - Metric Notation Chapter 4 - Scientific Notation And Metric Prefixes
Партнерские ресурсы
Криптовалюты
Магазины
Хостинг
Разное
Теория по электронике
Постоянный ток
Основные концепты электричества • Статическое электричество • Проводники, диэлектрики и поток электронов • Что такое электрические цепи • Напряжение и электроток • Сопротивление • Напряжение и электроток в реальной цепи • Условный ток и поток электронов
Закон Ома • Закон Ома – Как напряжение, сила тока и сопротивление связаны друг с другом • Аналогия для закона Ома • Мощность в электрических цепях • Расчёт электрической мощности • Резисторы • Нелинейная проводимость • Построение цепи • Полярность перепада напряжения • Компьютерная симуляция электрических цепей
Правила электробезопасности • Важность правил электробезопасности • Воздействие электричества на психологическое состояние • Путь, который ток проходит перед ударом • Закон Ома (снова!) • Техника безопасности • Первая медицинская помощь при ударе током • Распространённые источники опасности • Проектирование электроцепей с учётом требований безопасности • Безопасное использование приборов для измерения электрических показателей • Данные о влиянии удара током на тело человека
Экспоненциальная запись и метрические приставки • Экспоненциальная запись • Арифметические операции для экспоненциальной записи • Метрические обозначения • Преобразование метрических приставок • Используем ручной калькулятор • Экспоненциальная форма в программе SPICE
Последовательные и параллельные электрические цепи • Что такое «последовательные» и «параллельные» электрические цепи • Простая последовательная цепь • Простая параллельная цепь • Электропроводность • Рассчитываем мощность • Правильно используем закон Ома • Анализ отказов компонентов цепи • Строим простые резистивные цепи
Схемы с делителями напряжения и правила Кирхгофа • Схемы с делителем напряжения • Правило напряжений Кирхгофа (ПНК) • Цепи – делители тока и формула делителя тока • Правило Кирхгофа для силы тока (ПКТ)
Комбинированные последовательно-параллельные схемы • Что такое последовательно-параллельная цепь • Методы анализа последовательно-параллельных резисторных цепей • Перерисовываем избыточно усложнённые схемы • Анализ отказов компонентов (продолжение) • Построение простых резисторных цепей
Измерения в электрических цепях постоянного тока • Что такое измеритель? • Как устроен вольтметр • Как вольтметр влияет на измеряемую цепь • Как устроен амперметр • Как амперметр влияет на измеряемую цепь • Как устроен омметр • Высоковольтный омметр • Мультиметры • Кельвиновское 4-проводное измерение сопротивления • Мостовые схемы • Как устроен ваттметр • Как самостоятельно сделать ручной калибратор
Сигналы электрического оборудования • Аналоговые и цифровые сигналы • Системы сигналов напряжения • Системы сигналов силы тока • Тахогенераторы • Теромопары • Измерения pH • Тензодатчики
Анализ сети постоянного тока • Что такое сетевой анализ? • Метод токов ветвей • Аналитический метод контурных токов • Метод узловых потенциалов • Введение в сетевые теоремы • Теорема Миллмана • Теорема о суперпозиции • Теорема Тевенена • Теорема Нортона • Эквивалентность схем Тевенена и Нортона • И вновь о теореме Миллмана • Теорема о передаче максимальной мощности • Δ-Y и Y-Δ преобразования
Батареи и системы питания • Поведение электронов при химических реакциях • Батарейные конструкции • Рейтинг батарей • Батареи специального назначения • Практические рекомендации при использовании батарей
Физика проводников и диэлектриков • Введение в физику проводников и диэлектриков • Размеры проводов• Допустимые токовые нагрузки на провода • Предохранители • Удельное сопротивление • Температурный коэффициент сопротивления • Сверхпроводимость • Пробивное напряжение диэлектрика
Конденсаторы • Электрическое поле и ёмкость • Конденсаторы и дифференциальное исчисление • Факторы, влияющие на ёмкость конденсатора • Последовательное и параллельное соединение конденсаторов • Практические соображения - Конденсаторы
Магнетизм и электромагнетизм • Постоянные магниты • Электромангетизм • Единицы измерения магнитных величин • Магнитная проницаемость и насыщение • Электромагнитная индукция • Взаимная индукция
Катушки индуктивности • Магнитные поля и индуктивность • Катушки индуктивности и дифференциальное исчисление • Факторы, влияющие на индуктивность • Катушки индуктивности в последовательных и параллельных соединениях • Практические соображения – Катушки индуктивности
Постоянные времени в RC и L/R цепях • Переходные процессы в электрических цепях • Переходные процессы в цепях с конденсатором • Переходные процессы в цепях с катушкой индуктивности • Расчёт напряжения и силы тока • Почему L/R, а не LR? • Комплексные расчёты напряжения и тока • Сложные схемы • Расчёт неизвестного времени
Переменный ток
Основы теории переменного тока • Что такое переменный ток? • Формы волн переменного тока • Измерение величин переменного тока • Расчёт простейшей цепи переменного тока • Фаза переменного тока • Принципы радио
Комплексные числа • Введение в комплексные числа • Векторы и волны переменного тока • Сложение простых векторов • Сложение сложных векторов • Полярная и алгебраическая запись комплексных чисел • Арифметика комплексных чисел • И ещё по поводу полярности переменного тока • Несколько примеров с цепями переменного тока
Реактанс и импеданс – Индуктивность • Резистор в цепи переменного тока (Индуктивность) • Катушка индуктивности в цепи переменного тока • Последовательные резистивно-индуктивные цепи • Параллельные резистивно-индуктивные цепи • Особенности катушек индуктивности • Что такое «скин-эффект»?
Реактанс и импеданс – Ёмкость • Резистор в цепи переменного тока (Ёмкость) • Конденсатор в цепи переменного тока • Последовательные резистивно-ёмкостные цепи • Параллельные резистивно-ёмкостные цепи • Особенности конденсаторов
Реактанс и импеданс – R/L/C-цепи • Обзор R, X и Z (сопротивление, реактанс и импеданс) • Последовательные R/L/C-цепи • Параллельные R/L/C-цепи • Последовательно-параллельные R/L/C-цепи • Реактивная проводимость и адмиттанс • R/L/C-цепи – что в итоге?
Резонанс • Электрический маятник • Простой параллельный резонанс (колебательный контур) • Простой последовательный резонанс • Применение резонанса • Резонанс в последовательно-параллельных цепях • Добротность и полоса пропускания резонансной цепи
Сигналы переменного тока смешанной частоты • Сигналы переменного тока смешанной частоты - Введение • Прямоугольные волновые сигналы • Другие волновые формы • Подробнее о спектральном анализе • Эффекты в электрических цепях
Фильтры • Что такое фильтр? • Низкочастотные фильтры • Высокочастотные фильтры • Полосовые фильтры • Полосно-заграждающие фильтры • Резонансные фильтры • Подводя итоги по фильтрам
Трансформаторы • Взаимная индуктивность и основные операции • Повышающие и понижающие трансформаторы • Электрическая изоляция • Фазировка • Конфигурации обмотки • Регулировка напряжения • Специальные трансформаторы и приложения • Практические соображения – Трансформаторы
Многофазные цепи переменного тока • Однофазные системы питания • Трёхфазные системы питания • Чередование фаз • Устройство многофазного двигателя • Трёхфазные Y- и дельта-конфигурации • Трёхфазные цепи с трансформатором • Гармоники в многофазных энергосистемах • Гармонические фазовые последовательности
Коэффициент мощности • Мощность в резистивных и реактивных цепях переменного тока • Истинная, реактивная и полная мощность • Расчёт коэффициента мощности • Практическая коррекция коэффициента мощности
Измерение цепей переменного тока • Вольтметры и амперметры переменного тока • Измерение частоты и фазы • Измерение мощности • Измерение качества электроэнергии • Мостовые схемы переменного тока • Измерительные преобразователи переменного тока
Двигатели переменного тока • Введение в двигатели переменного тока • Синхронные двигатели • Синхронный конденсатор • Двигатель с магнитным сопротивлением • Шаговые двигатели • Бесщёточный двигатель постоянного тока • Многофазные асинхронные двигатели Теслы • Асинхронные двигатели с фазным ротором • Однофазные асинхронные двигатели • Прочие специализированные двигатели • Сельсин-двигатели (синхронизированные двигатели) • Коллекторные двигатели переменного тока
Линии передачи • Кабель на 50 Ом? • Электрические цепи и скорость света • Характеристический импеданс • Линии передачи конечной длины • «Длинные» и «короткие» линии передачи • Стоячие волны и резонанс • Преобразование импеданса • Волноводы
Полупроводники
Усилители и активные устройства • От электрики к электронике • Активные и пассивные устройства • Усилители • Коэффициент усиления • Децибелы • Абсолютные дБ-шкалы • Аттенюаторы
Теория твердотельных приборов • Введение в теорию твердотельных устройств • Квантовая физика • Валентность и кристаллическая структура • Зонная теория твёрдых тел • Электроны и «дырки» • P-N-переход • Полупроводниковые диоды • Транзисторы с биполярным переходом • Полевые транзисторы • Полевые транзисторы с изолированным затвором (MOSFET) • Тиристоры • Методы производства полупроводников • Сверхпроводящие устройства • Квантовые устройства • Полупроводниковые приборы в SPICE
Диоды и выпрямители • Диоды и выпрямители – Введение • Проверка диодов мультиметром • Номинальные характеристики диодов • Схемы выпрямителей • Пиковый детектор • Схемы ограничителей напряжения • Схемы фиксаторов уровня • Умножители напряжения (удвоители, утроители, учетверители и т.д.) • Схемы коммутации индуктивных нагрузок • Диодные схемы коммутации • Что такое диод Зенера (стабилитрон)? • Диоды специального назначения • Прочие диодные технологии • Модели диодов в SPICE
Биполярные транзисторы • Транзисторы с биполярным переходом (ТБП) – Введение • Транзистор с биполярным переходом (ТБП) как переключатель • Проверка транзистора с биполярным переходом (ТБП) с помощью мультиметра • Активный режим работы транзистора с биполярным переходом (ТБП) • Усилительный каскад с общим эмиттером • Усилительный каскад с общим коллектором • Усилительный каскад с общей базой • Каскодный усилитель • Методы смещения для транзисторов с биполярным переходом (ТБП) • Расчёт смещения для транзисторов с биполярным переходом (ТБП) • Взаимодействие входа и выхода в транзисторах с биполярным переходом (ТБП) • Обратная связь в транзисторах с биполярным переходом (ТБП) • Импеданс усилителя • Токовые зеркала в транзисторах с биполярным переходом (ТБП) • Параметры и корпуса транзисторов с биполярным переходом (ТБП) • Особенности транзисторов с биполярным переходом (ТБП)
Полевые транзисторы • Полевые транзисторы (JFET) – Введение • Полевой транзистор (JFET) как переключатель • Проверка полевого транзистора (JFET) с помощью мультиметра • Активный режим работы полевого транзистора (JFET)
Полевые транзисторы с изолированным затвором • Полевые транзисторы с изолированным затвором – Введение • Обедняющие полевые транзисторы с изолированным затвором • Биполярные транзисторы с изолированным затвором
Тиристоры • Гистерезис • Газоразрядные лампы • Диод Шокли (динистор) • DIAC (симметричный динистор) • Управляемый кремниевый выпрямитель (SCR-тиристор) • TRIAC (симметричный тринистор, триак) • Оптотиристоры • Однопереходной транзистор • Управляемый кремниевый коммутатор (SCS-тиристор) • Тиристоры с полевым управлением
Операционные усилители • Операционные усилители (ОУ) – Введение • Несимметричные и дифференциальные усилители • «Операционный» усилитель • Отрицательная обратная связь • Делитель напряжения в цепи обратной связи • Аналогия для делителя напряжения в цепи обратной связи • Преобразование сигнала напряжения в сигнал тока • Схемы усреднителя и сумматора • Построение дифференциальных усилителей • Инструментальный (измерительный) усилитель • Схемы дифференциатора и интегратора • Положительная обратная связь • Практические аспекты ОУ • Модели операционных усилителей
Практические аналоговые полупроводниковые схемы • Электростатический разряд • Схемы источников питания • Схемы усилителей • Осцилляторные схемы • Радиосхемы • Вычислительные схемы • Измерительные схемы
Приводы двигателей постоянного тока • Широтно-импульсная модуляция
Электронные лампы • Электронные лампы – Введение • История электронных ламп – с чего всё началось • Триод • Тетрод • Силовой лучевой тетрод • Пентод • Комбинированные электронные лампы • Характеристики электронных ламп • Ионизированные (газовые) электронные лампы • Индикаторные электронные лампы • Микроволновые электронные лампы • Сравниваем электронные лампы и полупроводники
Цифровая электроника
Системы счисления • Числа и способы их выражения • Системы счисления • Сравниваем десятеричные и двоичные числа • Восьмеричная и шестнадцатеричная системы счисления • Восьмеричные и шестнадцатеричные числа преобразовываем в десятеричные • Преобразование из десятеричной системы счисления
Двоичная арифметика • Числа и системы счисления • Двоичное сложение • Отрицательные двоичные числа • Двоичное вычитание • Двоичное переполнение • Наборы битов
Логические вентили • Цифровые сигналы и вентили • Вентили «НЕ» • «Буферные» вентили • Вентили с более чем одним входом • Транзисторно-транзисторная логика вентилей «И-НЕ» и «И» • Транзисторно-транзисторная логика вентилей «ИЛИ-НЕ» и «ИЛИ» • Схемы КМОП-вентилей • Специальные выходы в вентилях • Универсальность вентилей «И-НЕ» и «ИЛИ-НЕ» • Уровни напряжения для «высоких» и «низких» логических сигналов • Вентильные DIP корпусы
Переключатели • Типы переключателей • Как устроены контакты переключателей • «Нормальное» состояние контакта и последовательное замыкание/размыкание • «Дребезжание» контактов
Электромеханические реле • Устройство реле • Контакторы • Реле с задержкой времени • Защитные реле • Твердотельные реле
Релейная логика • «Лестничные» диаграммы • Функции цифровой логики • Разрешающие и блокирующие схемы • Схемы управления двигателем • Отказоустойчивость • Программируемые логические контроллеры (ПЛК)
Булева алгебра • Булева алгебра – Введение • Логическая арифметика • Булевы алгебраические тождества • Булевы алгебраические свойства • Логические правила для упрощения • Примеры упрощения схем • Функция «Исключающее ИЛИ»: вентиль XOR • Законы де Моргана • Преобразование таблиц истинности в логические выражения
Карты Карно • Карты Карно – Введение • Диаграммы Венна и множества • Булевы соотношения на диаграммах Венна • Преобразование диаграмм Венна в карты Карно • Карты Карно, таблицы истинности и логические выражения • Упрощение логики с помощью карт Карно • Бо́льшие карты Карно с 4-мя переменными • Минтермы и макстермы в реализациях • Обозначения сумм и произведений • Поля «безразличия» на картах Карно • Бо́льшие карты Карно с 5-ю и 6-ю переменными
Функции комбинационной логики • Функции комбинационной логики – Введение • Неполный сумматор • Полный сумматор • Декодер • Кодер • Демультиплексоры • Мультиплексоры • Совместное использование множественных комбинационных схем
Мультивибраторы • Цифровая логика с обратной связью • SR-защёлка • Вентильная SR-защёлка • D-защёлка • Защёлки с запуском по фронту сигнала: триггеры • JK-триггер • Триггеры с асинхронными входами • Моностабильные мультивибраторы
Схемы последовательностей • Двоичная счётная последовательность • Асинхронные счётчики • Синхронные счётчики • Конечные автоматы
Сдвиговые регистры • Сдвиговые регистры – Введение • Сдвиговые регистры: последовательный вход, последовательный выход (SISO) • Сдвиговые регистры: параллельный вход, последовательный выход (PISO) • Сдвиговые регистры: последовательный вход, параллельный выход (SIPO) • Универсальные сдвиговые регистры: параллельный вход, параллельный выход (PIPO) • Кольцевые счётчики
Цифро-аналоговые и аналого-цифровые преобразования • Цифро-аналоговые (ЦАП) и аналого-цифровые (АЦП) преобразования – Введение • ЦАП R/2nR: цифро-аналоговый преобразователь с двоично-взвешенным входом • ЦАП R/2R: (цифро-аналоговый преобразователь) • Параллельные АЦП • Цифровые ступенчатые АЦП • АЦП с последовательным приближением • Отслеживающий АЦП • Скатные (интегрирующие) АЦП • Дельта-сигма АЦП • Практические аспекты схем АЦП
Цифровая связь • Цифровая связь – Введение • Сети и шины • Потоки данных • Типы электрических сигналов • Оптическая передача данных • Топология сети • Сетевые протоколы • Практические аспекты цифровой связи
Цифровое хранилище (память) • Почему «цифровое»? • Понятия и концепции цифровой памяти • Современная немеханическая память • Устаревшие немеханические технологии памяти • Постоянное запоминающее устройство (ПЗУ) • Память с движущимися частями: «Приводы»
Принципы цифровых вычислений • Двоичный сумматор • Таблицы поиска • Конечные автоматы • Микропроцессоры • Микропроцессорное программирование
Справочные материалы
Полезные уравнения и коэффициенты пересчёта • Уравнения и законы для цепей постоянного тока • Правила последовательных цепей • Правила параллельных цепей • Эквивалентные значения компонентов в последовательных и параллельных цепях • Уравнение ёмкости конденсатора • Уравнение катушки индуктивности • Уравнения постоянной времени • Уравнения цепей переменного тока • Уравнения для децибел • Метрические приставки и преобразования единиц измерения
Цветовая маркировка • Цветовая маркировка резисторов • Цветовая маркировка проводки • Инфографика цветовой маркировки проводки
Таблицы проводников и диэлектриков • Таблица калибров медной проволоки • Таблица допустимых нагрузок для медного провода • Коэффициенты удельного сопротивления • Таблица температурных коэффициентов сопротивления • Критические температуры для сверхпроводников • Диэлектрическая прочность изоляторов
Справочник по алгебре • Основные алгебраические тождества • Основные свойства арифметики • Свойства степеней • Извлечение корней • Важные константы • Логарифмы • Формулы сокращённого умножения • Квадратное уравнение • Прогрессии • Факториалы • Решение систем уравнений: метод подстановки и метод сложения
Справочник по тригонометрии • Тригонометрия прямоугольного треугольника • Тригонометрия произвольного треугольника • Тригонометрические формулы • Гиперболические функции
Справочник по исчислению • Формулы вычисления пределов • Производная числа • Общие производные • Производные показательных функций с основанием e • Производные простых тригонометрических функций • Правила вычисления производных • Первообразная (неопределённый интеграл) • Общие первообразные • Первообразные показательных функций от числа e • Правила вычисления первообразных • Определённые интегралы и основная теорема исчисления • Дифференциальные уравнения
Использование программы SPICE для моделирования электрических схем • Программа моделирования электрических цепей SPICE — Введение • История программы SPICE • Основы программирования в SPICE • Интерфейс командной строки • Компоненты электрических схем • Опции для проведения анализа • Странные особенности программы SPICE • Примеры электрических цепей и списков связей
Устранение неполадок – теория и практика • Вопросы, которые следует задать, прежде чем продолжить • Общие советы по устранению неполадок • Конкретные методы устранения неполадок • Вероятные сбои в проверенных системах • Вероятные сбои в непроверенных системах • Возможные ментальные ловушки
Схематические обозначения элементов цепи • Провода и соединения • Источники питания • Типы резисторов • Типы конденсаторов • Катушки индуктивности • Взаимные катушки индуктивности • Переключатели с ручным управлением • Управляемые процессом переключатели • Переключатели с электрическим приводом (реле) • Соединители • Диоды • Биполярные транзисторы • Переходные транзисторы с полевым эффектом (JFET) • Транзисторы с полевым эффектом с изолированным затвором (IGFET или MOSFET) • Гибридные транзисторы • Тиристоры • Интегральные схемы • Электронные лампы
Периодическая таблица химических элементов • Таблица Менделеева
Эксперименты
Введение • Электроника как точная наука • Обустраиваем домашнюю лабораторию
Основные концепции и испытательное оборудование • Использование вольтметра • Использование омметра • Очень простая схема • Использование амперметра при измерении силы тока • Закон Ома • Нелинейное сопротивление • Рассеяние мощности • Цепь с переключателем • Эксперимент по электромагнетизму • Эксперимент с электромагнитной индукцией
Электрические цепи постоянного тока • Электрические цепи постоянного тока – Введение • Последовательные источники питания • Параллельные источники питания • Делитель напряжения • Делитель тока • Потенциометр как делитель напряжения • Потенциометр как реостат • Прецизионный потенциометр • Ограничение диапазона реостата • Термоэлектричество • Мультиметр своими руками • Чувствительный детектор напряжения • Потенциометрический вольтметр • 4-проводное измерение сопротивления • Простейший компьютер • Картошка-батарейка • Зарядка и разрядка конденсатора • Индикатор скорости изменения
Электрические цепи переменного тока • Электрические цепи переменного тока – Введение • Трансформатор – блок питания • Сборка трансформатора • Переменный индуктор • Чувствительный аудиодетектор • Обнаружение магнитных полей переменного тока • Обнаружение электрических полей переменного тока • Альтернатор – автомобильный генератор • Асинхронный двигатель • Асинхронный двигатель побольше • Фазовый сдвиг • Погашение звука • Музыкальный синтезатор как генератор сигналов • ПК-осциллограф • Анализ волновых сигналов • Колебательный контур • Сигнальная связь
Дискретные полупроводниковые схемы • Дискретные полупроводниковые схемы – Введение • Коммутирующий диод • Полупериодный выпрямитель • Двухполупериодный мостовой выпрямитель • Двухполупериодный выпрямитель с центральным отводом • Цепь «выпрямитель/фильтр» • Регулятор напряжения • Транзистор как переключатель • Датчик статического электричества • Датчик импульсного света • Повторитель напряжения • Усилитель с общим эмиттером • Многокаскадный усилитель • Как построить схему токового зеркала • JFET – регулятор тока • Дифференциальный усилитель • Простой операционный усилитель • Аудио осциллограф • Ламповый аудио усилитель
Аналоговые интегральные схемы • Аналоговые интегральные схемы – Введение • Компаратор напряжения • Прецизионный повторитель напряжения • Неинвертирующий усилитель • Высокоимпедансный вольтметр • Интегратор • Аудио осциллограф на таймерной схеме 555 • Наклонный генератор на таймерной схеме 555 • ШИМ-контроллер мощности • Аудиоусилитель класса B
Цифровые интегральные схемы • Цифровые интегральные схемы – Введение • Основная функция вентилей • SR-защёлка на основе вентилей «ИЛИ-НЕ» • SR-защёлка на основе вентиля «И-НЕ» с входом разрешения • SR-триггер на основе вентиля «И-НЕ» • Светодиодный секвенсор • Простейший кодовый замок • 3-битный двоичный счётчик • 7-сегментный дисплей
Таймерные схемы 555 • Интегральный таймер 555 • Триггер Шмитта на интегральном таймере 555 • Гистерезисный осциллограф на интегральном таймере 555 • Моностабильный мультивибратор на интегральном таймере 555 • Минимальное количество комплектующих для КМОП-схемы 555 проблескового прибора длительного действия на красных светодиодах • КМОП-схема 555 проблескового прибора длительного действия на синих светодиодах • КМОП-схема 555 проблескового прибора длительного действия на светодиодах обратного хода • КМОП-схема 555 проблескового прибора длительного действия на красных светодиодах

←Экспоненциальная запись и метрические приставки→
Источник — http://wikihandbk.com/ruwiki/index.php?title=Электроника:Постоянный_ток/Экспоненциальная_запись_и_метрические_приставки/Метрические_обозначения&oldid=7737726