Электроника:Полупроводники/Теория твердотельных приборов/Квантовая физика
Квантовая физика[1]
| « |
Полагаю, можно смело утверждать, что ни один человек в мире не понимает квантовую механику. | » |
| — Физик Ричард П. Фейнман | ||
Вряд ли будет преувеличением сказать, что изобретение полупроводниковых устройств было революцией. Это оказалось не только впечатляющим технологическим достижением, но проложило путь для технологий, которые кардинально изменили современное общество. Полупроводниковые устройства сделали возможным создание миниатюрной электроники, включая компьютеры, определённые типы медицинского оборудования для диагностики и лечения, а также популярные телекоммуникационные устройства, и это лишь то, что вспомнилось навскидку.
За этой технологической революцией стоит ещё бо́льшая революция в фундаментальной науке: в области квантовой физики. Без этого качественного скачка в понимании природы разработка полупроводниковых устройств (и более совершенных электронных устройств, которые всё ещё находятся в стадии разработки) была бы невозможна. Квантовая физика - невероятно сложная область науки. Эта глава – лишь поверхностный обзор. Когда ученые уровня Фейнмана говорят, что «никто не понимает [чего-то]», то можете не сомневаться, что это сложный предмет. Однако без хотя бы базового понимания квантовой физики или, по крайней мере, понимания научных открытий, которые привели к её формулировке, невозможно вообще понять, за счёт чего работают полупроводниковые электронные устройства. Большинство вводных в учебниках по электронике, которые я читал, пытаются объяснить полупроводники с точки зрения «классической» физики, что приводит скорее к путанице, чем к пониманию.
Атом
Многие из нас видели схематичные изображения атомов, вроде такого:

Крошечные частицы вещества, протоны и нейтроны, составляют центр атома; электроны движутся по своим орбитам, аки планеты вокруг звёзд. Ядро несёт положительный электрический заряд из-за присутствия протонов (нейтроны не имеют никакого электрического заряда), в то время как уравновешивающий отрицательный заряд атома находится во вращающихся электронах. Отрицательные электроны притягиваются к положительным протонам, как планеты за счёт гравитации притягиваются к Солнцу, но орбиты стабильны из-за движения электронов. Этой популярной моделью атома мы обязаны работе Эрнеста Резерфорда, который примерно в 1911 году экспериментально определил, что положительные заряды атомов сосредоточены в крошечном плотном ядре (а не равномерно распределены по диаметру атома), что предсказал ещё раннее другой исследователь – Дж. Дж. Томпсон.
Рассеяние Резерфорда
Эксперимент, в ходе которого обнаружилось т.н. рассеяние Резерфорда состоял в бомбардировке тонкой золотой фольги положительно заряженными альфа-частицами. Молодые аспиранты Х. Гейгер и Э. Марсден получили неожиданные результаты. Всего несколько альфа-частиц при прохождении сквозь фольгу отклонились на большие углы. Ещё меньше альфа-частиц отскочили в обратном направлении, развернув свою траекторию почти на 180°. Подавляющее же большинство частиц прошли через препятствие без малейших отклонений, как будто на их пути никакой фольги и не было. Тот факт, что только для движения нескольких альфа-частиц наблюдались существенные отклонения, указывал на присутствие крошечного положительно заряженного ядра.

Хотя атомная модель Резерфорда, учитывавшая эти экспериментальные данные, была лучше, чем предыдущая модель Томпсона, она всё же была далека до идеала. Дальнейшие попытки определить структуру атома проложили дорогу к странным открытиям квантовой физики. Современное понимание структуры атома несколько сложнее. Тем не менее, несмотря на дальнейшую революцию в квантовой физике и её вклад в наше понимание атомной структуры, наивная «планетарная» модель атома, предложенная Резерфордом, настолько укоренилась в общественном сознании, что до сих пор встречается в некоторых научных исследованиях, иногда даже в тех случаях, когда это совершенно неуместно.
Рассмотрим это краткое описание электронов в атоме, взятое из популярного учебника по электронике:
Таким образом, вращающиеся на своих орбитах отрицательные электроны притягиваются к положительному ядру, что подводит нас к вопросу, почему электроны не падают на ядро атома. Ответ заключается в том, что вращающиеся электроны остаются на своей стабильной орбите из-за двух равных, но противоположных сил. Центробежная сила тянет электроны за внешние пределы орбиты, и противодействует центростремительной силе, притягивающей электроны к ядру из-за разноимённых зарядов.
По заветам Резерфорда этот автор изображает электроны как твёрдые кусочки материи, вращающиеся по круговым орбитам, их внутреннее притяжение к противоположно заряженному ядру уравновешивается их движением. Пассаж про «центробежную силу» сам по себе технически неверен (даже если взять не электроны, а планеты), но легко простителен из-за того что модель Резерфорда прочно укоренилась, а на самом деле, вообще не существует такого понятия, как сила отталкивания любого орбитального тела в сторону от его орбитального центра. Это только кажется так, а на самом деле инерция тела поддерживает его прямолинейное движение, но поскольку орбитальное вращение – это постоянное отклонение (т.е. ускорение) от движения по прямой, то имеет место постоянное инерционное противодействие любой (центростремительной) силе, притягивающей тело к центру орбиту, будь то сила тяжести, электростатическое притяжение или даже механическое натяжение нити.
Но главная проблема подобных объяснений в том, что согласно им электроны якобы движутся по круговым орбитам. Ещё во времена Резерфорда подтверждён факт, что ускоряющиеся электрические заряды испускают электромагнитное излучение. Поскольку вращение по орбите – это разновидность движения с ускорением (вращающийся объект постоянно ускоряется, отклоняясь от обычного прямолинейного движения), электроны должны испускать излучение, наподобие тому, как вылетает грязь из-под вращающихся колёс. Это подтверждено экспериментально для электронов, ускоренных по круговой траектории в ускорителях частиц, называемых синхротронами (испускаемое излучение называется синхротронным излучением). Однако если электроны теряют энергию подобным образом, то это неизбежно должно приводить к разрушению их орбит и тогда в конечном счёте электроны должны падать на положительно заряженное ядро. Тем не менее, в атомах, как правило, этого не происходит. В реальности электронные «орбиты» удивительно стабильны в широком диапазоне условий.
Возбуждённые атомы
Более того, эксперименты с «возбуждёнными» атомами показали, что электромагнитная энергия, излучаемая атомом, возникает только на определённых, фиксированных частотах. Известно, что атомы, которые «возбуждаются» за счёт внешнего воздействия (например, если «выстрелить» в атом фотоном света), поглощают эту энергию и возвращают её в виде электромагнитных волн определённой частоты, наподобие тому, как камертон звенит с одной и той же высотой звука, независимо от того, как по нему ударить. Если свет, излучённый возбуждённым атомом, разделить с помощью призмы на составляющие его частоты (цвета́), то в спектре появятся отчётливые цветовые линии, причём структура спектральных линий будет уникальна для химического элемента этого атома. Это явление обычно используется для идентификации химических элементов и даже для измерения пропорций каждого элемента в соединении или химической смеси. Согласно резерфордовской «планетарной» атомной модели атома (где электроны рассматриваются как кусочки материи, свободно вращающиеся на орбите произвольного радиуса) и законам классической физики, возбуждённые атомы должны возвращать энергию в практически безграничном диапазоне частот, а не в нескольких избранных частотах. Другими словами, будь модель Резерфорда верна, не было бы эффекта «камертона», и световой спектр, излучаемый любым атомом, выглядел бы как непрерывная цветная полоса, а не как несколько отдельных линий.
Боровская модель атома

Исследователь-новатор Нильс Бор попытался улучшить «планетарную» модель после того, как провёл несколько месяцев в лаборатории Резерфорда в 1912 году. Пытаясь согласовать выводы других физиков (прежде всего Макса Планка и Альберта Эйнштейна), Бор предположил, что каждый электрон обладает строго определённым, конкретным количеством энергии. При этом орбиты электронов квантованы таким образом, что каждая из них может занимать определённые места вокруг ядра. Это можно уподобить шарикам, закреплённых на круговых траекториях вокруг ядра, а не свободно перемещающиеся спутники, как раннее предполагалось. Отдавая дань уважения законам электромагнетизма и ускоряющих зарядов, Бор называл эти «орбиты» стационарными состояниями, чтобы избежать любых намёков на то, что там есть какое-либо плавное движение. Хотя амбициозная попытка Бора переформулировать структуру атома в терминах, приближённых к экспериментальным результатам того времени, была важной вехой в физике, однако до истинного понимания структуры атома было ещё очень далеко. Математический анализ датского учёного более точно предсказывал результаты экспериментов, чем выкладки предыдущих моделей. И тем не менее всё ещё оставались безответные вопросы по поводу странного поведения электронов. Теория, что электроны находятся в стационарных квантованных состояниях вокруг ядра, лучше объясняла экспериментальные данные, чем модель Резерфорда. Но не было ни малейшего понятия, что заставляет электроны придерживаться этих конкретных состояний. Минуло десятилетие и ответ на этот вопрос дал другой физик, Луи де Бройль.
Волновая гипотеза де Бройля
Де Бройль предположил, что электроны, словно фотоны (частицы света), проявляют как свойства частиц, так и волновые свойства. Исходя из этого, он проанализировал вращающиеся электроны как волны, а не как частицы, что позволило лучше понять их квантовую природу. Действительно, это был ещё один прорыв.

Согласно де Бройлю, атом состоит из электронов, существующих в виде стоячих волн, и это явление хорошо известно физикам в самых разных формах. Словно это щипковая струна музыкального инструмента, колеблющаяся на резонансной частоте, с «узлами» и «пучностями» в стабильных положениях по её длине. Де Бройль представил электроны вокруг атомов, в виде стоячих волн, изогнутых по кругу:

Электроны могли существовать только на определённых, точных «орбитах» вокруг ядра, потому что только в этом случае есть совпадающие точки волн. Волна любого другого радиуса начинает интерферировать сама с собой, что приводит к её разрушению и, таким образом, она перестаёт существовать. Волновая гипотеза де Бройля с одной стороны хорошо объясняла математически, а с другой – давала удобную физическую аналогию для объяснения квантованных состояний электронов внутри атома. Но и эта атомная модель всё ещё была неполной. В течение нескольких последующих лет физики Вернер Гейзенберг и Эрвин Шрёдингер независимо друг от друга пришли к концепции корпускулярно-волнового дуализма в волновой гипотезе де Бройля, что позволило разработать математически более строгие модели для субатомных частиц.
Квантовая механика
Теоретический прогресс, от примитивной модели стоячей волны де Бройля до матриц Гейзенберга и дифференциальных уравнений Шрёдингера, ознаменовал появление квантовой механики и привнёс в мир субатомных частиц то, что повергло учёных в смятение: вероятность и неопределённость. Согласно новой квантовой теории, невозможно одновременно определить и точное положение частицы, и её точный импульс. Некоторое время была популярна точка зрения, что «принцип неопределенности» – это ошибка измерения (т.е. пытаясь точно измерить положение электрона, вы влияете на его импульс и, таким образом, нельзя определить импульс до измерения положения, и наоборот). Однако самое поразительное в квантовой механике то, что у любой микрочастицы и на самом деле нет и точного положений и точного импульса, а скорее выдерживается баланс обеих величины таким образом, что их совокупная неопределённость никогда не уменьшается ниже определённого минимального значения.
Подобная относительная «неопределённость» существует не только в квантовой механике. Если помните, мы уже сталкивались с взаимоисключающей взаимосвязью между достоверностью данных во временной области волны и её данными в частотной области (том II «Переменный ток», глава 7 «Сигналы переменного тока смешанной частоты», раздел 2 «Прямоугольные волновые сигналы»). Попросту говоря, чем точнее мы знаем составляющие частоты, тем менее точно известна амплитуда во времени для волны. И наоборот. Самоцитата:
Если у волны бесконечная продолжительность (бесконечное количество циклов), то анализ будет сделан с абсолютной точностью. И чем меньше циклов доступно компьютеру для анализа, тем менее точным будет анализ... Чем меньше повторных циклов у волны, тем с меньшей определённостью можно говорить о её частоте. Если довести эту концепцию до логического предела, короткий импульс (по сути, это волна, которая даже не завершает и один цикл) на самом деле вообще не имеет частоты, а действует как бесконечный диапазон частот. Этот принцип является общим для любых волновых явлений, а не только для переменного напряжения и тока.
Чтобы точно определить амплитуду изменяющегося сигнала, нужно дискретизировать его в пределах очень узкого промежутка времени. Однако это ограничивает наши сведения о частоте волны. И наоборот, чтобы определить частоту волны с большой точностью, её нужно дискретизировать в течении многих циклов, что означает, что мы теряем из виду её амплитуду в любой конкретный момент. Таким образом, мы не можем одновременно узнать мгновенную амплитуду и общую частоту любой волны с любой точностью. Ещё более странно то, что эта неопределённость существенно больше, чем погрешность наблюдений; эта неопределённость заложена в саму природу волны. Так что нельзя сказать, что если бы мы обладали соответствующей технологией, то смогли бы одновременно точно измерить и мгновенную амплитуду и частоту волны. В буквальном смысле волна не может иметь одновременно точную мгновенную амплитуду и точную частоту.
Минимальная неопределённость положения и импульса частицы, выраженная Гейзенбергом и Шредингером, не имеет ничего общего с ограничениями самих измерений; скорее, это внутреннее свойство дуализма, заложенного в саму природу материализованной волны, коей является микрочастица. Значит, электроны на самом деле находятся на своих «орбитах» не как точно определённые частицы материи или даже не как точно определённые волновые формы, а скорее как электронное «облако» – это такой технический термин для волновой функции распределения вероятностей, как если бы любой электрон «распределён» или «размазан» в диапазоне месторасположений и импульсов.
Поначалу кажется, что сей радикальный взгляд на электроны как на зыбкие облака противоречит первоначальному принципу квантованных электронных состояний: электроны существуют на дискретных, то бишь определённых «орбитах» вокруг атомных ядер. В конце концов, именно это открытие и привело к созданию объясняющей поведение электрона квантовой теории. Как-то странным кажется то, что теория, разработанная для объяснения дискретного поведения электронов, в конечном итоге объявляет, что электроны существуют в виде «облаков», а не как отдельные кусочки материи. Однако квантованное поведение электронов зависит не от самих электронов, имеющих определённые значения положения и импульса, а, скорее, от других свойств, называемых квантовыми числами. По своей сути, квантовая механика вообще не использует привычные в обычной механике понятия абсолютного положения и абсолютного импульса и заменяет их абсолютными понятиями, не имеющими аналогий в нашем повседневном опыте.
Четыре квантовых числа
Хотя электроны рассматриваются как существующие в некоем эфирном поле, «облаке» (рассматриваемом как форма распределенной вероятности), а не как отдельные кусочки материи, эти «облака» имеют другие характеристики, являющиеся дискретными. Любой электрон в атоме можно описать четырьмя числовыми мерами (упомянутые чуть выше, как квантовые числа): главное, орбитальное, магнитное и спиновое. Ниже приводится краткое описание каждого из этих чисел:
1. Главное квантовое число
Главное квантовое число: обозначаемое буквой n, это число описывает оболочку, в которой находится электрон. Электронная «оболочка» – это область пространства вокруг ядра атома, в которой допустимо нахождение электронов, дабы соответствовать устойчивой «стоячей волне» де Бройля и Бора. Электроны мгновенно «перепрыгивают» с оболочки на оболочку, но не могут ни в какой момент времени находиться где-то между этими оболочками. Главное квантовое число – это всегда положительное целое число (большее или равное 1). Другими словами, главное квантовое число для электрона не может быть равным 1/2 или -3. Эти целочисленные значения взяты не с потолка, а получены путём экспериментального подтверждения спектров света: разные частоты (цвета́) света, излучаемые возбуждёнными атомами водорода, соответствуют последовательности, математически зависящей от конкретных целочисленных значений, как показано на рисунке 3 выше.
На каждой оболочке может быть более одного электронов. Неплохая аналогия для электронных оболочек – концентрические зрительские ряды в амфитеатре. Подобно тому, как человек, сидящий в амфитеатре, должен выбрать ряд, где он хочет сесть (по правилам приличного театра сидеть между рядами нельзя), так и электрон должен «выбрать» конкретную оболочку, чтобы «сесть» в неё. Как и в рядах амфитеатра, являющихся самыми обширными, внешние оболочки содержат больше электронов, чем внутренние. Кроме того, электроны стремятся занять самую низкую доступную оболочку, так же как и люди в амфитеатре предпочитают место поближе к главной сцене. Чем выше номер оболочки, тем больше энергия у электронов в ней.
Максимальное количество электронов, которое может содержать любая оболочка, описывается уравнением 2n2, где «n» – главное квантовое число. Таким образом, первая оболочка (n = 1) может содержать максимум 2 электрона; вторая оболочка (n = 2) – 8 электронов, а третья оболочка (n = 3) – 18 электронов:

Электронные оболочки в атоме раньше обозначались буквой, а не цифрой. Первая оболочка (n = 1) отмечена как K, вторая оболочка (n = 2) как L, третья оболочка (n = 3) как M, четвертая оболочка (n = 4) как N, пятая оболочка (n = 5) как O, шестая оболочка (n = 6) как P и седьмая оболочка (n = 7) как Q.
2. Орбитальное (азимутальное) квантовое число
Орбитальное квантовое число: Каждая оболочка состоит из подоболочек. Можно утрированно сказать, что подоболочки это секции оболочек, напоминающие разделительные полосы на автобане. Подоболочки гораздо более странные, чем оболочки. Подоболочки – это области пространства, в которых могут существовать электронные «облака», при этом разные подоболочки различаются по форме. Первая подоболочка имеет форму сферы (рисунок 7(s)), что вполне имеет осмысленный вид при визуализации электрона в виде облака, окружающего атомное ядро в трёх измерениях. Вторая подоболочка, однако, уже напоминает какую-то гантель, состоящую из двух «лепестков», имеющих точку соединения рядом с центром атома (рисунок 7(p)). Третья подоболочка обычно напоминает набор из четырёх «лепестков», сгруппированных вокруг ядра атома. Эти формы подоболочки напоминают графические изображения мощности сигнала радиоантенны.с выпуклыми лепестками, отходящими от антенны в разных направлениях. (Рисунок ниже (d))

Допустимые квантовые орбитальные числа являются целыми положительными числами (как и главные квантовые числа), но среди возможных значений есть и ноль. Эти квантовые числа для электронов обозначены буквой l (маленькая латинская «эль»). Количество подоболочек в оболочке равно главному квантовому числу оболочки. Таким образом, первая оболочка (n = 1) имеет одну подоболочку с номером 0; вторая оболочка (n = 2) имеет две подоболочки, пронумерованные как 0 и 1; третья оболочка (n = 3) имеет три подоболочки, пронумерованные как 0, 1 и 2.
Изначально для описания подоболочек использовались буквы, а не числа. В этой системе обозначении первая подоболочка (l = 0) обозначена s, вторая подоболочка (l = 1) обозначена p, третья подоболочка (l = 2) обозначена d, а четвертая подоболочка (l = 3) обозначена f. Буквы происходят от слов резкий (sharp), главный (principal, при этом не стоит путать с главным квантовым числом n), диффузный (diffuse) и фундаментальный (fundamental). Эта система по-прежнему часто встречается во многих периодических таблицах, используемая для обозначения электронной конфигурации внешних или валентных оболочек атома:

3. Магнитное квантовое число
Магнитное квантовое число: для электрона определяет ориентацию его подоболочки. «Лепестки» подоболочек могут быть по-разному ориентированы в пространстве. Эти разные ориентации называются орбиталями. Первая подоболочка (s; l = 0) сфероподобна, т.е. фактически не выделено какое-то конкретное направление, поэтому существует только одна орбиталь. Вторая подоболочка (p; l = 1) в каждой оболочке, напоминает по форме гантель, которая в трёхмерном пространстве может быть ориентирована в трёх возможных направлениях. Представьте себе три гантели, пересекающиеся в начале координат, каждая из которых ориентирована по разным осям в трехосном координатном пространстве.
Допустимые числовые значения для этого квантового числа состоят из целых чисел от -l до l и обозначаются символами ml в атомной физике и lz в ядерной физике. Чтобы вычислить количество орбиталей в любой заданной подоболочке, удвойте номер подоболочки и добавьте 1 (2 × l + 1). Например, первая подоболочка (l = 0) в любой оболочке содержит одну орбиталь, пронумерованную как 0 (2 × 0 + 1 = 1); вторая подоболочка (l = 1) в любой оболочке содержит три орбитали, пронумерованные как -1, 0 и 1 (2 × 1 + 1 = 3); третья подоболочка (l = 2) содержит пять орбиталей, пронумерованных как -2, -1, 0, 1 и 2 (2 × 2 + 1 = 5); и так далее.
Как и все основные квантовые числа, магнитное квантовое число определено непосредственно из экспериментальных данных. Название «магнитное» квантовое число связано с изучением эффекта Зеемана, при котором наблюдается расщепление спектральных линий атома в результате воздействия магнитного поля на ионизированный газ.
4. Спиновое квантовое число
Спиновое квантовое число: как и магнитное квантовое число, это свойство атомных электронов обнаружено экспериментально. Дотошное изучение спектральных линий показало, что каждая линия на самом деле была парой очень близко расположенных линий. Обнаружение этой так называемой тонкой структуры позволило выдвинуть гипотезу о том, что каждый электрон в некотором роде «вращается» вокруг собственной оси, словно планета. Электроны с разными «спинами» при возбуждении испускают импульсы света, имеющих немного разную частоту. Этому квантовому числу было присвоено название «спин» (что дословно переводится с английского как «вращение»). Стоит понимать, что концепция «вращающегося» электрона в настоящее время устарела и, скорее подходит для (неверного) представления об электронах как о дискретных кусочках материи, а не как об «облаках»; но название остаётся.
Спиновые квантовые числа обозначаются символами ms в атомной физике и sz в ядерной физике. Для каждой орбитали в каждой подоболочке в каждой оболочке может быть два электрона, один со спином +½, а другой со спином -½.
Принцип исключения (запрета) Паули
Физик Вольфганг Паули сформулировал правило, объясняющий упорядочение электронов в атоме в соответствии с их квантовыми числами. Этот принцип исключения Паули (или принцип запрета Паули), гласит, что никакие два электрона в одном атоме не могут находиться в одинаковых квантовых состояниях. То есть каждый электрон в атоме имеет уникальный набор квантовых чисел. Это ограничивает количество электронов, которые могут занимать любую заданную орбиталь, подоболочку или оболочку.
Здесь показано расположение электронов в атоме водорода:
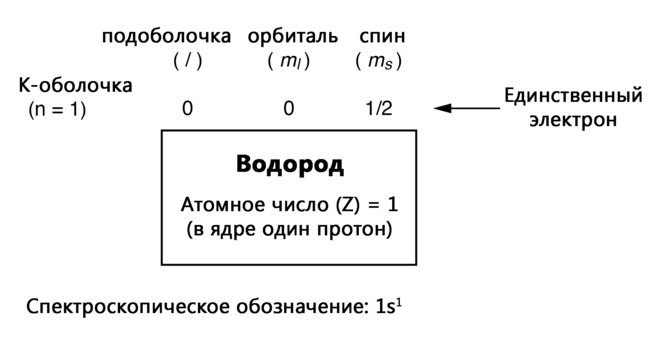
С одним протоном в ядре требуется только один электрон, чтобы электростатически уравновесить атом (положительный электрический заряд протона точно уравновешен отрицательным электрическим зарядом электрона). Этот единственный электрон находится в самой нижней оболочке (n = 1), в первой подоболочке (l = 0), на единственной орбитали (пространственной ориентации) этой подоболочки (ml = 0) со значением спина ½. Распространённый метод описания этой организации – перечисление электронов в соответствии с их оболочками и подоболочками в соглашении, называемом спектроскопическим обозначением. В этом обозначении номер оболочки показывается как целое число, подоболочка – как буква (s, p, d, f), а общее количество электронов в подоболочке (все орбитали, все спины) - как верхний индекс. Таким образом, в атоме водорода, единственный электрон, находящийся на базовом уровне, описывается как 1s1.
Если перейдём к следующему атому (со следующим порядковым номером), получаем элемент гелий:

У атома гелия два протона в ядре, и это требует наличия двух электронов, чтобы уравновесить двойной положительный электрический заряд. Поскольку два электрона (один со спином +½, а другой со спином -½) помещаются на одну орбиталь, электронная конфигурация гелия не требует дополнительных подоболочек или оболочек для второго электрона.
Но если в атоме три или более электронов, то непременно потребуются дополнительные подоболочки для удержания всех электронов, поскольку только два электрона поместятся в самую нижнюю оболочку (n = 1). Рассмотрим следующий атом в последовательности возрастающих атомных номеров, литий:

Атом лития лишь частично использует вместимость L-оболочки (n = 2). Эта оболочка фактически может содержать восемь электронов (максимальная вместимость L-оболочки = 2n2 электронов). Рассмотрим организацию атома с полностью заполненной L-оболочкой, чтобы увидеть, как все комбинации подоболочек, орбиталей и спинов заняты электронами:

Часто, когда для атома даются спектроскопические обозначения, любые полностью заполненные оболочки опускаются, в обозначении присутсвует только незаполненная оболочка или оболочка, заполненная на самом высоком уровне. Например, элемент неон (показанный на предыдущем рисунке), который имеет две полностью заполненные оболочки, может быть спектроскопически описан просто как 2p6, а не как 1s22s22p6. Литий с полностью заполненной K-оболочкой и единственным электроном в L-оболочке можно описать просто как 2s1, а не как 1s22s1.
Отсутствие полностью заполненных оболочек нижних уровней – используется не просто для удобства и сокращения записи. Это также иллюстрирует основной принцип химии: химическое поведение элемента в первую очередь определяется его незаполненными оболочками. И водород, и литий имеют по одному электрону на своих внешних оболочках (1s1 и 2s1 соответственно), что придаёт этим двум элементам некоторые схожие свойства. Оба являются высокореактивными веществами и вступают в реакцию схожим образом (соединение с аналогичными элементами происходит в аналогичных режимах). Не так существенно, что у лития есть полностью заполненная K-оболочка под почти пустой L-оболочкой: незаполненная L-оболочка – это оболочка, которая в основном и определяет его химическое поведение.
Элементы с полностью заполненными внешними оболочками классифицируются как благородные и отличаются практически полной инертностью по отношению к другим элементам. Эти элементы раньше классифицировались как инертные, поскольку когда-то считалось, что они полностью инертны, но теперь известно, что они образуют соединения с другими элементами при определённых условиях.
Периодическая таблица
Поскольку элементы с идентичными электронными конфигурациями в их внешней оболочке (оболочках) проявляют сходные химические свойства, Дмитрий Менделеев соответствующим образом организовал различные элементы в таблице. Такая таблица известна как периодическая таблица элементов, и современные таблицы в целом следуют этой общей форме:

Дмитрий Менделеев, русский химик, был первым, кто разработал периодическую таблицу элементов. Хотя Менделеев организовал свою таблицу в соответствии с атомной массой (а не атомным номером), и поэтому его таблица оказалась не настолько полезной, как современные периодические таблицы. Тем не менее, его разработка является прекрасным примером научного исследовательского метода. Увидев закономерности периодичности (сходные химические свойства в зависимости от атомной массы), Менделеев предположил, что все элементы должны вписываться в эту упорядоченную схему. Когда он обнаружил «пустые» места в таблице, он, следуя логике этой периодичности, выдвинул гипотезу о существовании пока ещё не открытых элементов. Последующее открытие этих элементов подкрепило гипотезу Менделеева, способствовало будущим открытиям и привело к той форме периодической таблицы, которую мы используем и поныне.
Вот так и должна работать наука: гипотезы доводятся до своих логических выводов и принимаются, изменяются или отклоняются, в зависимости от того, как эти выводы согласуются с экспериментальными данными. Задним умом все крепки: любой дурак может постфактум сформулировать гипотезу для объяснения уже существующих экспериментальных данных – и многие так и делают. В том и отличие научной гипотезы от апостериорной спекуляции – в предсказании будущих экспериментальных данных, которые ещё не собраны, и возможность опровержения теории, если она не согласуется с результатами этих данных. Смело довести гипотезу до её логического завершения и осмелиться предсказать результаты будущих экспериментов – это не догматический «прыжок веры», а, скорее, публичная проверка этой гипотезы, которая бросает вызов любому, кто способен предоставить опровергающие данные. Другими словами, выдвижение научных гипотез всегда предполагает определённый «риск» из-за того, что гипотеза претендует на предсказание результатов еще не проведённых экспериментов, и поэтому гипотезу можно опровергнуть, если выводы экспериментов не оправдают ожиданий. Таким образом, если гипотеза успешно предсказывает результаты повторных экспериментов, утверждается истинность гипотезы и отбрасывается её ложность.
Квантовая механика: от гипотез к теории
Квантовая механика возникла как гипотеза, затем развивалась как теория. Она оказалась чрезвычайно успешной в предсказании экспериментальных результатов, отсюда и высокая степень научного доверия к ней. Многие ученые резонно полагают, что это неполная теория, так как она хорошо предсказывает в масштабе микромира, но мало имеет отношения к реальности макроскопических размеров. И тем не менее это чрезвычайно полезная теория для объяснения и прогнозирования взаимодействий частиц и атомов.
Как вы уже увидели в этой главе, квантовая физика нужна для описания и предсказания многих различных явлений. В следующем разделе мы увидим её значение для электропроводности твёрдых веществ, включая полупроводники. Проще говоря, в химии или физике твёрдого тела далеко не уедешь если придерживаться популяризированных (и при этом ложных) представлений, согласно которым электроны существуют в виде дискретных кусочков материи, вращающихся вокруг атомных ядер, словно миниатюрные спутники. А вот, если электроны рассматриваются как «волновые функции», существующие в определённых дискретных состояниях, то это позволяет объяснить регулярное и периодическое поведение материи на микроуровне.
Итог
- Электроны в атомах существуют в «облачном» виде с распределённой вероятностью, а не в виде дискретных кусочков материи, вращающихся вокруг ядра, словно крошечные спутники, как нам ложно показывают обычные иллюстрации, на которых изображены атомы.
- Отдельные электроны вокруг атомного ядра имеют уникальные «квантовые состояния», описываемые четырьмя квантовыми числами: главное квантовое число, определяющее оболочку; орбитальное квантовое число, определяющее подоболочку; магнитное квантовое число, определяющее орбиталь (ориентацию подоболочки); и квантовое спиновое число, или просто спин. Эти состояния квантованы, что означает, что для электрона не существует никаких «промежуточных» условий, кроме тех состояний, которые вписываются в схему квантовой нумерации.
- Главное квантовое число (n) описывает базовый уровень или оболочку, в которой электрон находится. Чем больше это число, тем больше радиус электронного облака (т.е. тем больше расстояние от ядра атома) и тем больше энергия электрона. Основные квантовые числа являются положительными целыми числами.
- Орбитальное квантовое число (l) описывает форму электронного облака в пределах определённой оболочки или уровня, и часто известен как «подоболочка». В любой данной оболочке количество подоболочек (форм электронного облака) равно главному квантовому числу. Орбитальные квантовые числа – это натуральные числа, начинающиеся с нуля и заканчивающиеся на число, которое на единицу меньше главного квантового числа (n - 1).
- Магнитное квантовое число (ml) описывает пространственную ориентацию для подоболочки (формы электронного облака). Количество различных ориентаций для подоболочки равно двукратному числу подоболочки (l) плюс единица (2 × l + 1). Например, для l = 1, ml может принимать три значения (2 × 1 + 1 = 3) и быть равной -1, 0, 1. Каждая уникальная ориентация называется орбиталью. Эти числа представляют собой целые числа в диапазоне, начиная от отрицательного значения номера подоболочки (-l) до 0 и включительно до положительного значения номера подоболочки (+l).
- Спиновое квантовое число (ms) описывает другое свойство электрона, и может представлять собой значение +½ или -½.
- Принцип исключения Паули гласит, что никакие два электрона в атоме не могут иметь одинаковый набор квантовых чисел. Отсюда следует, что любая орбиталь не может содержать более двух электронов (у такой пары электронов почти все квантовые числа равны, за исключением того, что у одного спин = +½ , а у другого спин = -½. В каждой подоболочке может быть не более чем 2 × l + 1 орбиталей, а в каждой оболочке не более чем n подоболочек.
- Спектроскопические обозначения – это условное обозначение электронной конфигурации атома. Оболочки показаны целыми числами, за которыми следуют буквы, символизирующие подоболочки (s, p, d, f), а числа в верхнем индексе обозначают общее количество электронов, находящихся в каждой соответствующей подоболочке.
- Химическое поведение атома определяется исключительно электронами в незаполненных внешних оболочках. Полностью заполненные низкоуровневые оболочки практически не влияют на характеристики химической связи элементов.
- Элементы с полностью заполненными электронными оболочками почти полностью инертны и называются благородными (ранее назывались инертными).
См.также
Внешние ссылки