Processing:Справочник языка Processing/bezierTangent(): различия между версиями
Материал из Онлайн справочника
Перейти к навигацииПерейти к поиску
Нет описания правки |
Myagkij (обсуждение | вклад) Нет описания правки |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 1: | Строка 1: | ||
{{Processing панель перехода}} | {{Processing панель перехода}} | ||
{{Перевод от Сubewriter}} | {{Перевод от Сubewriter}} | ||
{{Myagkij-редактор}} | {{Myagkij-редактор}} | ||
= bezierTangent() <ref>[https://processing.org/reference/bezierTangent_.html processing.org - bezierTangent()]</ref>= | = bezierTangent() <ref>[https://processing.org/reference/bezierTangent_.html processing.org - bezierTangent()]</ref>= | ||
| Строка 99: | Строка 96: | ||
<references /> | <references /> | ||
{{Навигационная таблица/Портал/Processing}} | |||
{{Навигационная таблица/ | |||
Текущая версия от 15:24, 13 сентября 2023
| Содержание | Среда разработки Processing | Справочник языка Processing | Библиотеки | Примеры | Режимы программирования |
Перевод: Максим Кузьмин
Проверка/Оформление/Редактирование: Мякишев Е.А.
bezierTangent() [1]
Обозначение
bezierTangent()
Описание
Рассчитывает касательную прямую для точки внутри кривой Безье. Хорошее определение касательной прямой можно найти в «Википедии».
Синтаксис
bezierTangent(a, b, c, d, t)
Параметры
a – координаты первой опорной точки кривой Безье. Тип данных – float
b – координаты первой контрольной точки кривой Безье. Тип данных – float
c – координаты второй контрольной точки кривой Безье. Тип данных – float
d – координаты второй опорной точки кривой Безье. Тип данных – float
t – точка внутри кривой Безье; значение между «0» и «1». Тип данных – float
Возвращаемое значение
Тип данных – float.
Пример
№1
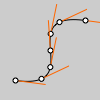
noFill();
bezier(85, 20, 10, 10, 90, 90, 15, 80);
int steps = 6;
fill(255);
for (int i = 0; i <= steps; i++) {
float t = i / float(steps);
// считываем координаты точки:
float x = bezierPoint(85, 10, 90, 15, t);
float y = bezierPoint(20, 10, 90, 80, t);
// считываем точки касания:
float tx = bezierTangent(85, 10, 90, 15, t);
float ty = bezierTangent(20, 10, 90, 80, t);
// на основе точек касания рассчитываем угол:
float a = atan2(ty, tx);
a += PI;
stroke(255, 102, 0);
line(x, y, cos(a)*30 + x, sin(a)*30 + y);
// закомментированная строчка кода ниже делает инверсию линии выше:
//line(x, y, cos(a)*-30 + x, sin(a)*-30 + y);
stroke(0);
ellipse(x, y, 5, 5);
}
№2

noFill();
bezier(85, 20, 10, 10, 90, 90, 15, 80);
stroke(255, 102, 0);
int steps = 16;
for (int i = 0; i <= steps; i++) {
float t = i / float(steps);
float x = bezierPoint(85, 10, 90, 15, t);
float y = bezierPoint(20, 10, 90, 80, t);
float tx = bezierTangent(85, 10, 90, 15, t);
float ty = bezierTangent(20, 10, 90, 80, t);
float a = atan2(ty, tx);
a -= HALF_PI;
line(x, y, cos(a)*8 + x, sin(a)*8 + y);
}
См.также
Внешние ссылки
| Примеры на Processing | |
|---|---|
| Основы |
|
| Продвинутые графические эффекты |
|
| Примеры из сторонних библиотек | |